[Algorithm] 순열 / 조합 개념과 알고리즘 구현
순열 Permutation
개념
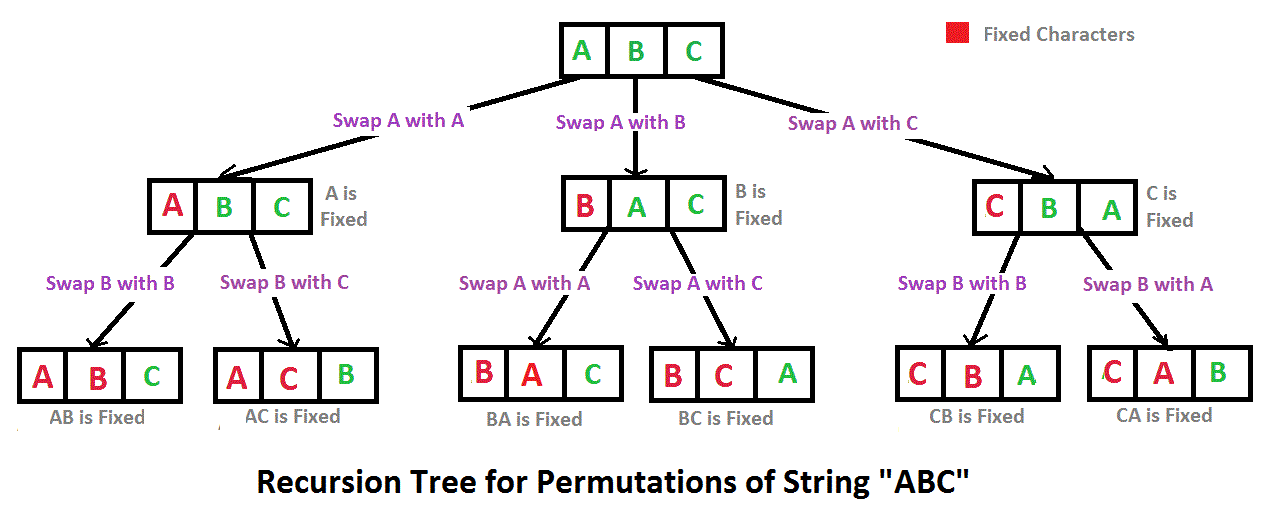
순열은 서로 다른 n개 요소 중에서 r개를 선택하여 순서대로 나열하는 방법을 의미한다. 순열에선 순서가 결과에 영향을 미치기 때문에 순서가 중요하다. 동일한 요소를 서로 다른 순서로 나열하면, 각각을 별개의 순열로 간주한다. 예를 들어 A, B, C에서 A, B 두 요소를 선택하는 경우 AB와 BA는 서로 다른 순열이다.
- A 선택, 남은 글자 B, C
- B 선택, 남은 글자 C (2자리 순열이므로 무시) →
AB - C 선택, 남은 글자 B (2자리 순열이므로 무시) →
AC
- B 선택, 남은 글자 C (2자리 순열이므로 무시) →
- B 선택, 남은 글자 A, C
- A 선택, 남은 글자 C (2자리 순열이므로 무시) →
BA - C 선택, 남은 글자 A (2자리 순열이므로 무시) →
BC
- A 선택, 남은 글자 C (2자리 순열이므로 무시) →
- C 선택, 남은 글자 A, B
- A 선택, 남은 글자 B (2자리 순열이므로 무시) →
CA - B 선택, 남은 글자 A (2자리 순열이므로 무시) →
CB
- A 선택, 남은 글자 B (2자리 순열이므로 무시) →
A, B, C 3가지 문자(n=3)로 만들 수 있는 2자리 순열(r=2)의 수는 총 6가지다. 첫 번째 자리에 올 수 있는 문자는 A, B, C 3가지를 선택할 수 있다. 두 번째 자리에는 남은 두 문자가 위치할 수 있으므로 2가지를 선택할 수 있다. 따라서 모든 순열의 수는 $3 \times 2 = 6$이 된다.

이처럼 순열은 각 단계에서 선택할 수 있는 모든 수를 곱한 것과 같으므로 팩토리얼의 개념을 부분적으로 포함하여 $n \times (n-1) \times (n-2) \times ... \times (n-r+1)$ 식으로 표현할 수 있다. 마지막 선택을 $n-r+1$로 표현한 이유는 r번째 요소를 선택할 시점은 r-1개의 요소를 선택한 상태이기 때문이다.
예를들어 n=5, r=3일 때 r(3)번째 요소를 선택할 차례에선 이미 r-1(2)개의 요소를 선택한 상태이다. 따라서 마지막 선택(r번째)의 남은 요소의 수는 n(5)에서 r-1(2)를 뺀 3이 된다. 이를 식으로 표현하면 $n-(r-1)$이 되고 분배 법칙으로 단순화하면 $n-r+1$이 되는 것.
순열을 수학적 공식으로 표기하면 $P(n,r)=\frac{n!}{(n-r)!}$ 이 된다. $\frac{n!}{(n-r)!}$ 식을 계산해보면 $(n-r)!$에 해당하는 항은 약분된 후 지워져서 $n \times (n-1) \times (n-2) \times ... \times (n-r+1)$ 형태가 되기 때문이다.
$$P(3, 2) = \frac{3!}{(3-2)!} = \frac{3 \cdot 2 \cdot \cancel{1}}{\cancel{1}} = 3 \cdot 2 = 6$$
$$P(5, 3) = \frac{5!}{(5-3)!} = \frac{5 \cdot 4 \cdot 3 \cdot \cancel{2 \cdot 1}}{\cancel{2 \cdot 1}} = 5 \cdot 4 \cdot 3 = 60$$
💡 약분은 분자/분모가 공통된 인수를 가질 때, 이 인수로 분자와 분모를 나눠서 분수를 더 간단한 형태로 만드는 과정. ①분자/분모의 최대공약수(GCD)를 찾고, ②분자/분모를 최대공약수로 나눈 후, ③그 결과를 새로운 분자/분모에 사용하여 분수를 간소화한다. 다항식으로 된 분수는 분모와 분자를 인수분해(주어진 정수를 더 이상 나눌 수 없는 소수들의 곱으로 표현)하여 다항식(1개 이상의 항, e.g. 2x + 4는 항 2개)의 곱으로 나타낸 뒤 분자/분모에 모두 존재하는 다항식을 약분해서 없앤다.
💡 순열은 $P(n,r)$ 혹은 $_nP_r$로 표기할 수 있다. P는 영단어 Permutation의 첫 글자를 가리킨다.
실생활 예시
- 암호 생성 : 0~9까지 숫자로 4자리 암호를 설정할 때, 각 자리에 들어가는 숫자의 순서에 따라 결과가 달라진다. 예를들어 [1, 2, 3, 4]와 [4, 3, 2, 1]은 서로 다른 암호다.
- 순위 결정 : 스포츠 대회에서 A, B, C 선수가 각각 1등~3등을 차지하는 것과 C, B, A가 1등~3등을 차지하는 것은 전혀 다르다. 즉, 결승선에 먼저 들어온 순서에 따라 결과는 달라진다.
구현
const getPermutations = (arr, permSize = arr.length, curPerm = []) => {
// 현재 순열 길이가 요구하는 순열 크기와 같으면 현재 순열 반환 (Base Case)
if (curPerm.length === permSize) return [curPerm];
// 배열이 비어있거나 요구하는 순열 크기가 0이면 빈 배열 반환
if (arr.length === 0 || permSize === 0) return [];
return arr.reduce((allPerms, item, i) => {
const restItems = arr.slice(0, i).concat(arr.slice(i + 1));
const nextPerm = curPerm.concat(item);
return allPerms.concat(getPermutations(restItems, permSize, nextPerm));
}, []);
};
getPermutations(['A', 'B', 'C'], 2); // [['A', 'B'], ['A', 'C'], ...]- 입력받은 배열의 요소를 하나씩 선택하여
curPerm순열 배열에 추가한다 - 선택한 요소를 제외한 나머지 요소를
restItems배열(다음 순열 생성 단계에서 사용)에 저장한다 - 나머지 요소와 순열 배열을 사용하여 재귀적으로(1~2 과정 반복) 순열을 생성한다
- 재귀 과정을 통해 생성된 모든 순열을 하나의 배열로 만든 후 반환한다
조합 Combination
개념
조합은 서로 다른 n개 요소 중에서 순서에 상관없이 r개를 선택하는 방법을 의미한다. 조합에선 선택한 요소들의 순서를 고려하지 않는다. 예를 들어 A, B, C에서 A, B 두 요소를 선택하는 경우 AB와 BA는 동일한 조합으로 간주한다. 조합에선 중복을 피하기 위해 각 단계에서 선택한 요소 뒤에 있는 요소들만 조합의 대상으로 고려한다.
- A 선택, 남은 글자 B, C
- B 선택, 남은 글자 C (2자리 조합이므로 무시) →
AB - C 선택, 남은 글자 無 →
AC
- B 선택, 남은 글자 C (2자리 조합이므로 무시) →
- B 선택, 남은 글자 C
- C 선택, 남은 글자 無 →
BC
- C 선택, 남은 글자 無 →
- C 선택, 남은 글자 無
위처럼 A, B, C로 만들 수 있는 2자리 조합의 수는 3가지다. 조합은 순열과 달리 요소의 순서를 고려하지 않으므로, 동일한 요소들이 순서만 다른 경우를 한 그룹으로 묶어서 계산하면 조합의 수를 얻을 수 있다.
예를들어 A, B, C로 만들 수 있는 2자리(r=2) 순열은 AB, BA, AC, CA, BC, CB 총 6가지다. 이 순열에서 [AB, BA], [AC, CA], [BC, CB]와 같이 서로 순서만 다른 경우들을 그룹으로 묶어서 처리하면 조합이 된다.
각 그룹은 $r!$ 가지 방법으로 나열될 수 있는데, 한 조합(e.g. AB)의 순열은 두 가지(e.g. AB, BA)가 있다는 것을 의미한다. 따라서 순열의 총 수를 각 그룹의 순열 수인 $r!$로 나누면 중복을 제거한 조합의 수를 계산할 수 있다.

정리하면 n개 요소에서 r개를 선택하는 순열의 수($_nP_r$)를, $r!$로 나눠서 조합의 수($_nC_r$)를 구할 수 있다. 이를 수학적 공식으로 표기하면 $C(n,r) = \frac{_nP_r}{r!} =\frac{n!}{r!(n-r)!}$이 된다. $\frac{n!}{(n-r)!}$식은 순열을 나타내고, $(n-r)!$에 해당하는 항이 약분돼서 $\frac{_nP_r}{r!}$ 형태로 단순화된다.
$$C(3,2)=\frac{3!}{2!(3-2)!}=\frac{3 \cdot 2 \cdot \cancel{1}}{2 \cdot 1 \cdot \cancel {1}}=3$$
$$C(5,3)=\frac{5!}{3!(5-3)!}=\frac{5 \cdot 4 \cdot 3 \cdot \cancel{2} \cdot \cancel{1}}{3\cdot 2 \cdot 1 \cdot \cancel{2} \cdot \cancel{1}} =10$$
실생활 예시
- 로또 번호 : 45개 숫자 중에서 6개를 고르는 로또 추첨에서 각 숫자의 순서는 중요하지 않다. 숫자조합 [5, 12, 23, 34, 40, 42]와 [42, 34, 23, 12, 5, 40]은 동일한 결과로 취급한다.
- 조 배정 : 30명 중에서 5명으로 이뤄진 조를 구성할 때, 한 조에 속하는 사람의 순서는 중요하지 않다. 예를들어 [A, B, C, D, E] 그룹과 [E, D, C, B, A] 그룹은 동일하다.
구현
const getCombinations = (arr, combSize, start = 0, curComb = []) => {
if (curComb.length === combSize) return [curComb]; // 목표 크기의 조합을 완성했을 때
if (start === arr.length) return []; // 더이상 조합을 생성할 수 없을 때
return arr.slice(start).reduce((allCombs, item, i) => {
const nextComb = curComb.concat(item);
const nextStart = start + i + 1;
return allCombs.concat(getCombinations(arr, combSize, nextStart, nextComb));
}, []);
};
getCombinations(['A', 'B', 'C'], 2); // [['A', 'B'], ['A', 'C'], ['B', 'C']]/**
* Iteratively generates combinations from an array. This method is typically
* more performant than its recursive counterpart. For example, generating combinations of 2 elements
* from a 1000-element array takes about 100ms iteratively, compared to 600ms functionally.
*/
const getCombinationsIterative = (arr, combSize, start = 0, curComb = []) => {
if (curComb.length === combSize) return [curComb];
const results = [];
const maxIndex = arr.length - combSize + curComb.length;
for (let i = start; i <= maxIndex; i++) {
const nextComb = curComb.concat(arr[i]);
const nextStart = i + 1;
results.push(...getCombinationsIterative(arr, combSize, nextStart, nextComb));
}
return results;
};- 입력받은 배열의
start인덱스부터 요소를 하나씩 선택하여 현재 조합curComb에 추가한다 - 선택한 요소 뒤에 있는 요소들로 조합을 생성하기 위해
nextStart인덱스를 업데이트한다 - e.g.
['A', 'B', 'C']배열에서 선택한 요소가B(i=1)라면nextStart는 2가 된다 - 현재 조합과 업데이트한 인덱스를 사용하여 재귀적으로(1~2과정 반복) 조합을 생성한다
- 재귀 과정을 통해 생성된 모든 조합을 하나의 배열로 만든 후 반환한다
레퍼런스
글 수정사항은 노션 페이지에 가장 빠르게 반영됩니다. 링크를 참고해 주세요
'🪄 Programming' 카테고리의 다른 글
| [JS] 바닐라 자바스크립트로 마리오 러너 게임 구현하기 (0) | 2024.05.29 |
|---|---|
| [HTML] select, option 요소의 주요 속성과 특징 (0) | 2024.05.29 |
| [React] 리액트에서 setTimeout 더 편하게 쓰기 (0) | 2024.05.28 |
| [React] 크롬 확장 프로그램 개발 배경 지식 및 튜토리얼 (0) | 2024.05.28 |
| [Algorithm] 자바스크립트 Map으로 구현하는 LRU Cache 알고리즘 (0) | 2024.05.28 |
댓글
이 글 공유하기
다른 글
-
[JS] 바닐라 자바스크립트로 마리오 러너 게임 구현하기
[JS] 바닐라 자바스크립트로 마리오 러너 게임 구현하기
2024.05.29 -
[HTML] select, option 요소의 주요 속성과 특징
[HTML] select, option 요소의 주요 속성과 특징
2024.05.29 -
[React] 리액트에서 setTimeout 더 편하게 쓰기
[React] 리액트에서 setTimeout 더 편하게 쓰기
2024.05.28 -
[React] 크롬 확장 프로그램 개발 배경 지식 및 튜토리얼
[React] 크롬 확장 프로그램 개발 배경 지식 및 튜토리얼
2024.05.28

