[Algorithm] 프로그래머스 - 피로도 / 백트래킹으로 모든 부분집합 찾기
프로그래머스 레벨 2 피로도 문제는 던전 목록과 HP가 주어졌을 때 방문할 수 있는 최대 던전의 수를 반환해야 한다. 각 던전은 최소 피로도와 소모 피로도를 가진다. 최소 피로도는 해당 던전을 방문하기 위해 필요한 최소 HP를 의미하고, 소모 피로도는 말 그대로 해당 던전을 방문했을 때 소모되는 HP를 나타낸다. 문제에서 주어지는 매개변수는 아래와 같다.
k: 시작 HP. e.g.,80dungeons: [최소 피로도, 소모 피로도]로 이루어진 던전 목록. e.g.,[[80,20],[50,40],[30,10]]
최소 피로도와 소모 피로도가 각각 다르기 때문에 방문 순서에 따라 방문할 수 있는 던전의 수가 달라진다. 예를 들어 [[80,20],[50,40],[30,10]] 던전 목록에서 2~3번(i1~i2) 던전부터 방문하면 최대 2개 던전만 방문할 수 있다. 1번 던전(i0)의 최소 피로도가 80이기 때문에 다른 던전을 먼저 방문하면 HP가 80 미만이 되고 그럼 1번 던전의 최소 피로도를 만족하지 못하기 때문이다.
- 첫 번째 던전부터 방문했을 때 : 1 → 2 → 3 (최대 3개 던전)
- 두 번째 던전부터 방문했을 때 : 2 → 3 (최대 2개 던전)
- 세 번째 던전부터 방문했을 때 : 3 → 2 (최대 2개 던전)
순열을 이용한 방법
주어진 던전의 모든 가능한 순서를 탐색해봐야 하므로 던전 목록에 대한 순열(Permutation)을 생성한 뒤, 각 순열을 순회하면서 방문할 수 있는 최대 던전 개수를 계산하는 방식으로 해결했다.
const getPermutation = (arr, perm = [], max = 3) => {
if (perm.length === max) return [perm];
const result = [];
for (let i = 0; i < arr.length; i++) {
const newPerm = [...perm, arr[i]];
const rest = arr.slice(0, i).concat(arr.slice(i + 1));
result.push(...getPermutation(rest, newPerm, max));
}
return result;
};
function solution(k, dungeons) {
const perms = getPermutation(dungeons, [], dungeons.length);
let maxCount = 0;
for (const perm of perms) {
let currentK = k;
let count = 0;
for (const [requiredK, consumeK] of perm) {
if (currentK >= requiredK) {
currentK -= consumeK;
count++;
} else {
break;
}
}
maxCount = Math.max(count, maxCount);
}
return maxCount;
}
모든 순열의 개수는 $n!$ 이므로, getPermutation 함수의 시간 복잡도는 $O(n!)$ 이 된다. solution 함수에선 생성한 순열을 다시 한번 순회하므로 전체 코드의 시간 복잡도는 $O(n! \cdot n)$으로 비효율적이다. 만약 n이 10이라면 약 3600만 번의 연산이 필요하다.
백트래킹을 이용한 방법
💡 백트래킹, 순열은 모든 경우의 수를 탐색하여 답을 찾는 완전 탐색(Exhaustive Search)에 속한다.
백트래킹은 문제를 해결하기 위해 가능한 모든 경우의 수를 시도하면서, 조건에 맞지 않으면 탐색을 중단하고 이전 단계로 돌아가서 다른 가능성을 탐색하는 방법이다. 깊이 우선 탐색(DFS)과 유사하지만 불필요한 경로를 배제하는 가지치기(pruning) 과정을 통해 문제를 더 효율적으로 해결한다.
프로그래머스에서 좋아요를 가장 많이 받은 코드는 백트래킹을 이용해서 해결했다. 이 문제는 순열을 고려해야 하기 때문에 시간복잡도는 최악의 경우 $O(n!)$이지만 코드가 훨씬 깔끔해진다.
function solution(k, dungeons) {
const N = dungeons.length; // 던전 개수
const visited = new Array(N).fill(false); // 방문 여부를 추적하는 배열
let maxCount = 0;
function dfs(hp, count) {
maxCount = Math.max(count, maxCount);
for (let i = 0; i < N; i++) {
// 아직 방문하지 않은 던전이고, 던전의 최소 피로도를 만족하면
if (hp >= dungeons[i][0] && !visited[i]) {
visited[i] = true; // 방문 상태로 변경
dfs(hp - dungeons[i][1], count + 1);
visited[i] = false; // 미방문 상태로 변경 (백트래킹)
}
}
}
dfs(k, 0);
return maxCount;
}
위 코드의 작동 과정을 4단계로 정리하면 아래와 같다.
- 아직 방문하지 않은 던전이고, 던전의 최소 피로도를 만족하는지 검사한다.
- 조건을 만족하면
count,hp상태를 업데이트하고 던전을 방문한다. - 최대 방문 카운트(maxCount)를 업데이트한다.
- 방문 상태를 되돌리고(백트래킹), 다음 던전을 방문하는 과정을 반복한다.

k = 80, dungeons = [[80, 20], [50, 40], [30, 10]]
N = 3 | visited = [f, f, f] | maxCount = 0
===================================================================
⑴ dfs(80, 0)
maxCount = max(0, 0) = 0
i0 -> ⑵ dfs(80-20, 0+1) | visited = [t, f, f] -> visited = [f, f, f]
i1 -> ⑹ dfs(80-40, 0+1) | visited = [f, t, f] -> visited = [f, f, f]
i2 -> ⑻ dfs(80-10, 0+1) | visited = [f, f, t] -> visited = [f, f, f]
================================ i0 ================================
⑵ dfs(60, 1)
maxCount = max(1, 0) = 1
i0 -> pass(이미 방문)
i1 -> ⑶ dfs(60-40, 1+1) | visited = [t, t, f] -> visited = [t, f, f]
i2 -> ⑷ dfs(60-10, 1+1) | visited = [t, f, t] -> visited = [t, f, f]
⑶ dfs(20, 2)
maxCount = max(2, 1) = 2
i0~i2 pass
⑷ dfs(50, 2)
maxCount = max(2, 2) = 2
i0 -> pass(이미 방문)
i1 -> ⑸ dfs(50-40, 2+1) | visited = [t, t, t] -> visited = [t, f, t]
i2 -> pass(이미 방문)
⑸ dfs(10, 3)
maxCount = max(3, 2) = 3
i0~i2 pass
================================ i1 ================================
⑹ dfs(40, 1)
maxCount = max(1, 3) = 3
i0 -> pass(피로도 만족 못함)
i1 -> pass(이미 방문)
i2 -> ⑺ dfs(40-10, 1+1) | visited = [f, t, t] -> visited = [f, t, f]
⑺ dfs(30, 2)
maxCount = max(2, 3) = 3
i0~i2 pass
================================ i2 ================================
⑻ dfs(70, 1)
maxCount = max(1, 3) = 3
i0 -> pass(피로도 만족 못함)
i1 -> ⑼ dfs(70-40, 1+1) | visited = [f, t, t] -> visited = [f, f, t]
i2 -> pass(이미 방문)
⑼ dfs(30, 2)
maxCount = max(1, 3) = 3
i0~i2 pass
(번외) 부분집합 찾기
부분집합은 어떤 집합의 원소들 중 일부 또는 전체를 포함하는 집합을 의미한다. 집합 A의 모든 원소가 집합 B에 포함되어 있다면, 집합 A는 집합 B의 부분집합(Subset)이 되며, 기호는 $A \subset B$로 나타낸다.
부분집합은 원소 개수 0개부터 최대 원소 개수까지 포함할 수 있기 때문에 공집합과 자기 자신도 부분집합에 포함된다. 예를 들어 집합 {1, 2, 3, 4}의 부분 집합은 아래와 같다.
- 원소의 개수가 0개인 부분집합: 공집합 $\emptyset$
- 원소의 개수가 1개인 부분집합(1자리 조합): {1}, {2}, {3}, {4}
- 원소의 개수가 2개인 부분집합(2자리 조합): {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}
- 원소의 개수가 3개인 부분집합(3자리 조합): {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}
- 원소의 개수가 4개인 부분집합(자기 자신, 4자리 조합): {1, 2, 3, 4}
각 원소는 부분집합에 포함되거나 포함되지 않는 두 가지 선택을 가지므로, n개 원소에 대한 부분집합의 총개수는 $2 \times 2 \times \dots \times 2 = 2^n$개가 된다.
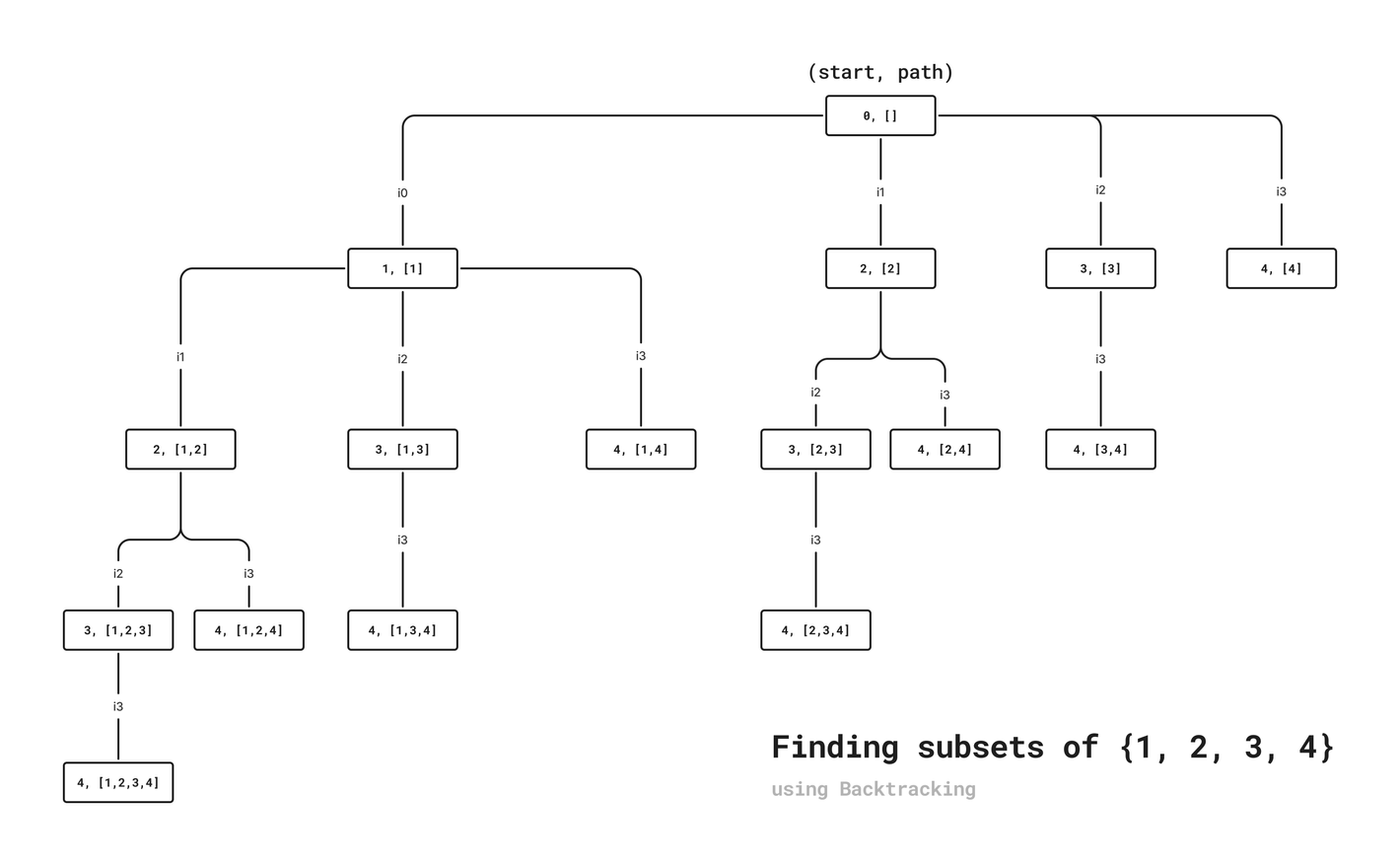
이처럼 부분집합은 주어진 집합의 원소들로 만들 수 있는 모든 가능한 조합(Combination)을 의미하기도 한다. 한편, 특정 집합의 모든 부분집합을 찾을 때도 백트래킹을 사용할 수 있다. 시간복잡도는 부분집합의 총개수와 동일한 $O(2^n)$이 된다.
function findSubsets(nums) {
const result = [];
function generateSubsets(start, path) {
result.push([...path]); // 현재 경로를 결과에 추가
for (let i = start; i < nums.length; i++) {
path.push(nums[i]); // 현재 원소를 경로에 추가
generateSubsets(i + 1, path); // 다음 원소 탐색
path.pop(); // 경로에서 마지막 원소 제거(백트래킹)
}
}
generateSubsets(0, []);
return result;
}
- 현재 경로의 복사본을
result에 추가한다 start인덱스에 있는 원소부터path에 추가하여 다음 원소를 탐색한다- 탐색을 마치면 마지막 원소를
path에서 제거한다(백트래킹) nums배열의 마지막 인덱스까지 위 과정을 반복한다.
nums = [1, 2, 3]
==============================================================
f(0, [])
result = [[]]
i0 -> path = [1] -> ⑴ f(0+1, [1]) -> path = []
i1 -> path = [2] -> ⑸ f(1+1, [2]) -> path = []
i2 -> path = [3] -> ⑺ f(2+1, [3]) -> path = []
⑴ f(1, [1])
result = [[], [1]]
i1 -> path = [1, 2] -> ⑵ f(1+1, [1, 2]) -> path = [1]
i2 -> path = [1, 3] -> ⑷ f(2+1, [1, 3]) -> path = [1]
⑵ f(2, [1, 2])
result = [[], [1], [1, 2]]
i2 -> path = [1, 2, 3] -> ⑶ f(2+1, [1, 2, 3]) -> path = [1, 2]
⑶ f(3, [1, 2, 3])
result = [[], [1], [1, 2], [1, 2, 3]]
skip loop
⑷ f(3, [1, 3])
result = [[], [1], [1, 2], [1, 2, 3], [1, 3]]
skip loop
⑸ f(2, [2])
result = [[], [1], [1, 2], [1, 2, 3], [1, 3], [2]]
i2 -> path = [2, 3] -> ⑹ f(2+1, [2, 3]) -> path = [2]
⑹ f(3, [2, 3])
result = [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3]]
skip loop
⑺ f(3, [3])
result = [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]
skip loop글 수정사항은 노션 페이지에 가장 빠르게 반영됩니다. 링크를 참고해 주세요
'🪄 Programming' 카테고리의 다른 글
| [Dart] 자바스크립트 개발자의 다트 학습 - Part 2 (1) | 2024.08.21 |
|---|---|
| [Dart] 자바스크립트 개발자의 다트 학습 - Part 1 (0) | 2024.08.21 |
| [DevTools] 리액트 테스트 환경(Vitest, React Testing Library) 및 CI 구축 (1) | 2024.07.22 |
| [JS] 자바스크립트 정규식으로 천 단위 구분자 추가하기 (단어 경계, 전후방탐색) (0) | 2024.07.18 |
| [JS] 자바스크립트 reduce() 메서드 활용 예시 모음 (0) | 2024.07.07 |
댓글
이 글 공유하기
다른 글
-
[Dart] 자바스크립트 개발자의 다트 학습 - Part 2
[Dart] 자바스크립트 개발자의 다트 학습 - Part 2
2024.08.21 -
[Dart] 자바스크립트 개발자의 다트 학습 - Part 1
[Dart] 자바스크립트 개발자의 다트 학습 - Part 1
2024.08.21 -
[DevTools] 리액트 테스트 환경(Vitest, React Testing Library) 및 CI 구축
[DevTools] 리액트 테스트 환경(Vitest, React Testing Library) 및 CI 구축
2024.07.22 -
[JS] 자바스크립트 정규식으로 천 단위 구분자 추가하기 (단어 경계, 전후방탐색)
[JS] 자바스크립트 정규식으로 천 단위 구분자 추가하기 (단어 경계, 전후방탐색)
2024.07.18