[JS] 자바스크립트 Set 객체의 집합 연산 메서드 (교집합, 합집합 등)
반응형
TL;DR
💡 ES6에 도입된 Set 객체는 중복을 허용하지 않는 고유한 값들을 저장하는 데이터 구조다. Set은 동일한 값을 두 번 저장할 수 없기 때문에 중복된 값을 추가하면 자동으로 무시한다. 또한 삽입 순서를 기억하고, 원시형과 참조형 값을 모두 지원한다 — 참고 포스팅
Firefox 127 버전부터 별도의 폴리필 없이 크롬(Chrome)을 포함한 대부분의 주요 브라우저 엔진에서 교집합, 합집합, 차집합 등 집합 연산을 수행하는 새로운 Set 메서드를 지원한다. 크로스 브라우저에서 지원하는 메서드는 다음과 같다.
A.intersection(B): 두 Set이 공통으로 가지는 요소를 포함한 새로운 Set 반환 — 교집합A.union(B): 두 Set이 가진 모든 요소를 포함한 새로운 Set 반환 — 합집합A.difference(B): A Set에는 있지만 B Set에는 없는 요소를 포함한 새로운 Set 반환 — 차집합A.symmetricDifference(B): 두 Set이 공통으로 가지는 요소를 제외한 새로운 Set 반환 — 대칭 차집합A.isSubsetOf(B): A Set의 모든 요소를 B Set이 포함하는지 여부 — A가 B의 부분 집합인지 여부A.isSupersetOf(B): A Set이 B Set의 모든 요소를 포함하는지 여부 — A가 B의 상위 집합인지 여부A.isDisjointFrom(B): 두 Set이 공통 요소를 가지지 않는지 여부 — 서로소 집합 여부
A.intersection(B) | 교집합
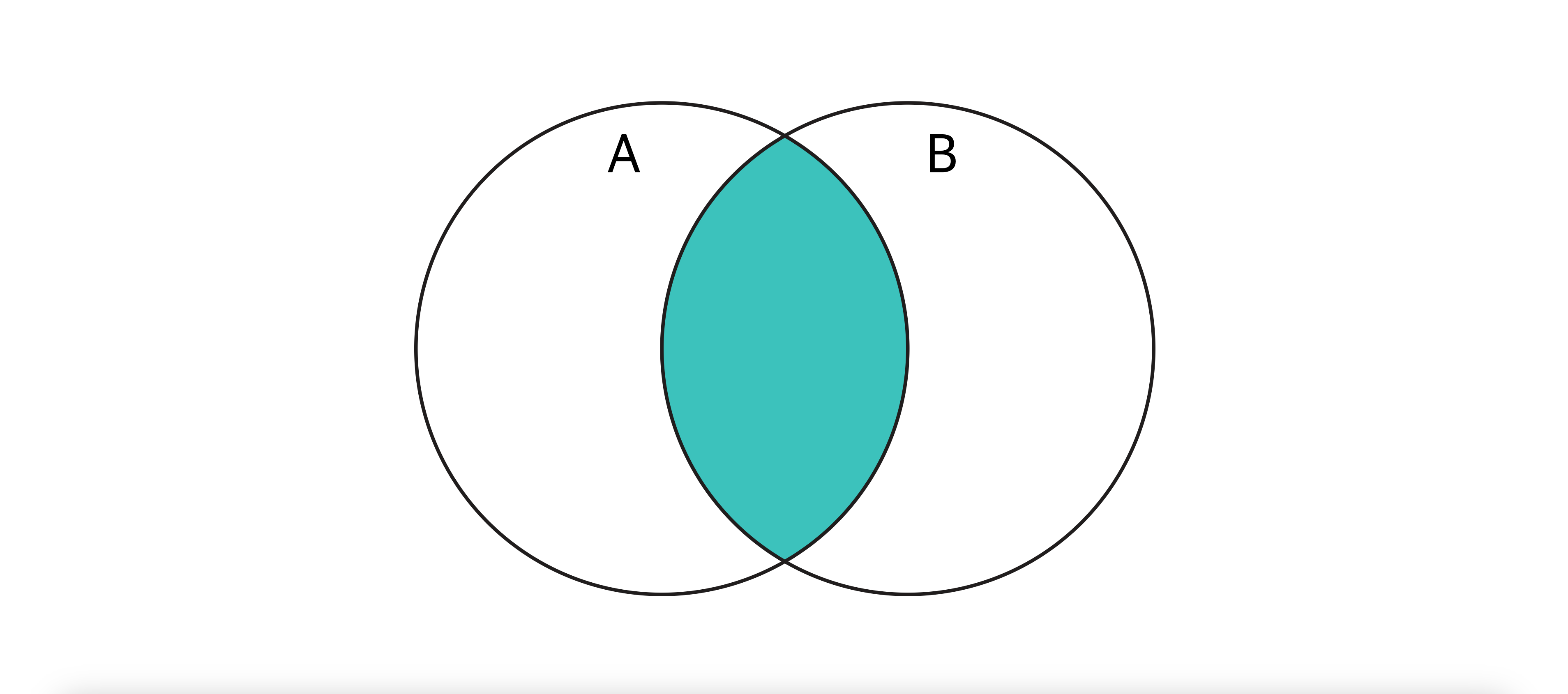
- 설명 : 두 Set이 공통으로 가지는 요소를 포함한 새로운 Set 반환
- 반환값 : Set
- 수학적 표기 : 𝐴∩𝐵 — A와 B가 모두 가지는 요소
- 참고 링크 : MDN | 활용 예시
const odds = new Set([1, 3, 5, 7, 9]);
const squares = new Set([1, 4, 9]);
console.log(odds.intersection(squares)); // Set(2) { 1, 9 }
A.union(B) | 합집합
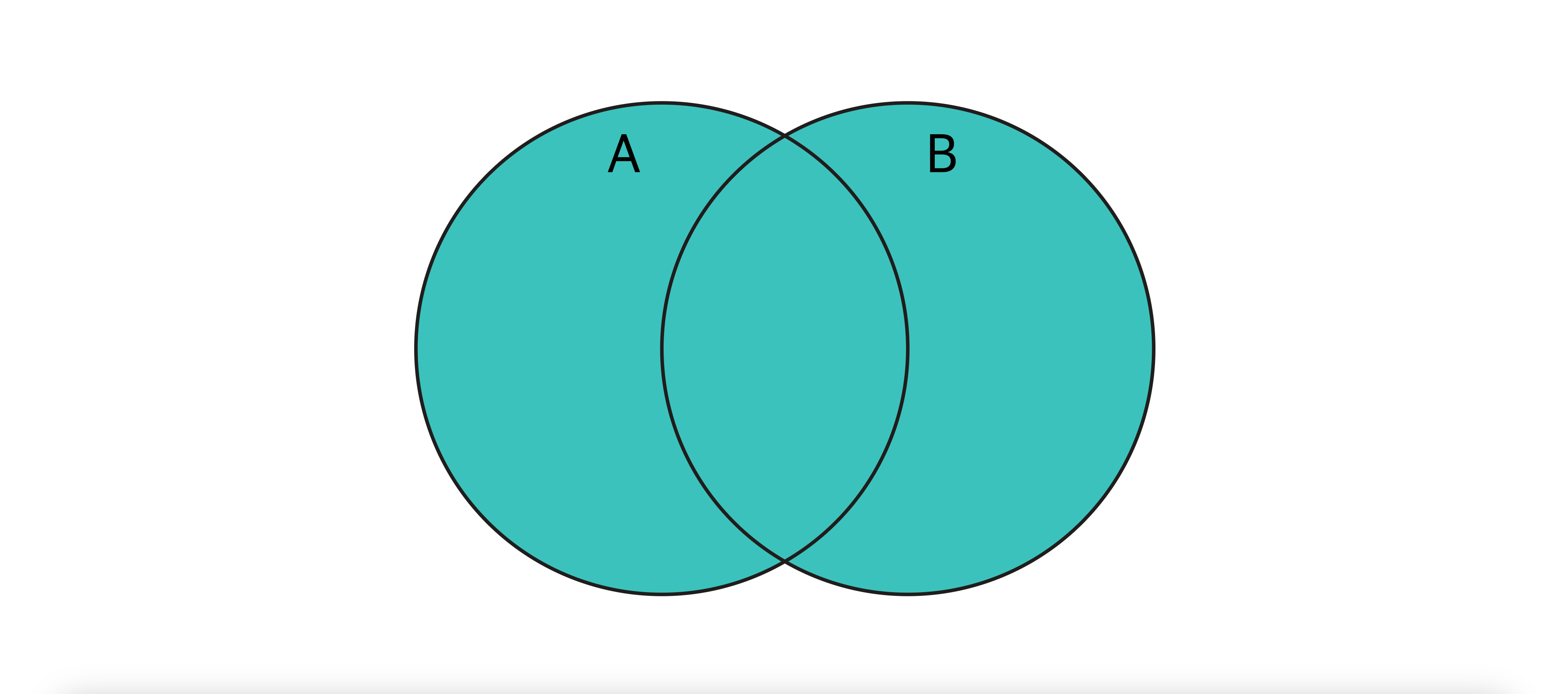
const evens = new Set([2, 4, 6, 8]);
const squares = new Set([1, 4, 9]);
console.log(evens.union(squares)); // Set(6) { 2, 4, 6, 8, 1, 9 }
A.difference(B) | 차집합
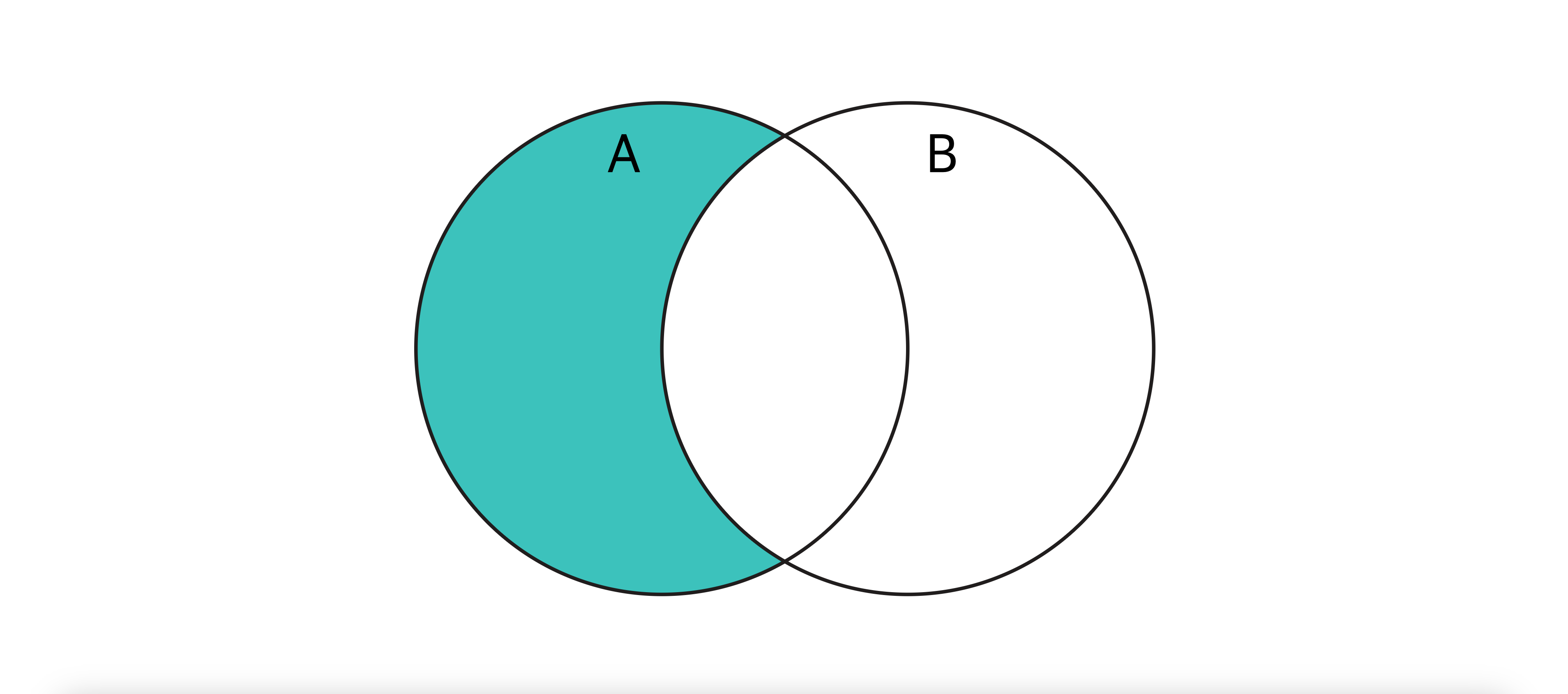
- 설명 : A Set에는 있지만 B Set에는 없는 요소를 포함한 새로운 Set 반환 (A Set에만 있는 요소)
- 반환값 : Set
- 수학적 표기 : 𝐴∖𝐵 — A에서 B를 뺀 요소
- 참고 링크 : MDN | 활용 예시
const odds = new Set([1, 3, 5, 7, 9]);
const squares = new Set([1, 4, 9]);
console.log(odds.difference(squares)); // Set(3) { 3, 5, 7 }
A.symmetricDifference(B) | 대칭 차집합
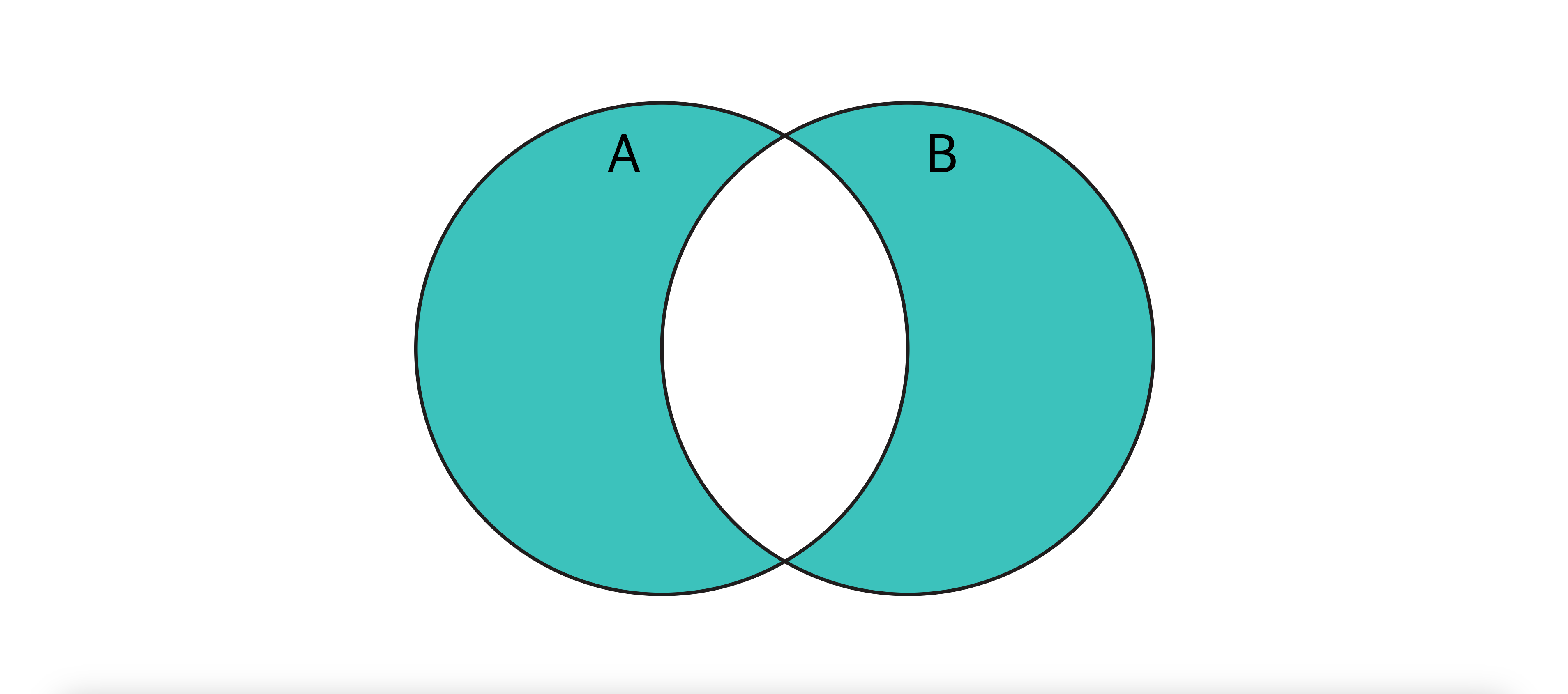
- 설명 : 두 Set이 공통으로 가지는 요소를 제외한 새로운 Set 반환
- 반환값 : Set
- 수학적 표기 : (𝐴∖𝐵)∪(𝐵∖𝐴) — A에서 B를 뺀 요소 + B에서 A를 뺀 요소
- 참고 링크 : MDN | 활용 예시
const evens = new Set([2, 4, 6, 8]);
const squares = new Set([1, 4, 9]);
console.log(evens.symmetricDifference(squares)); // Set(5) { 2, 6, 8, 1, 9 }
A.isSubsetOf(B) | 부분 집합
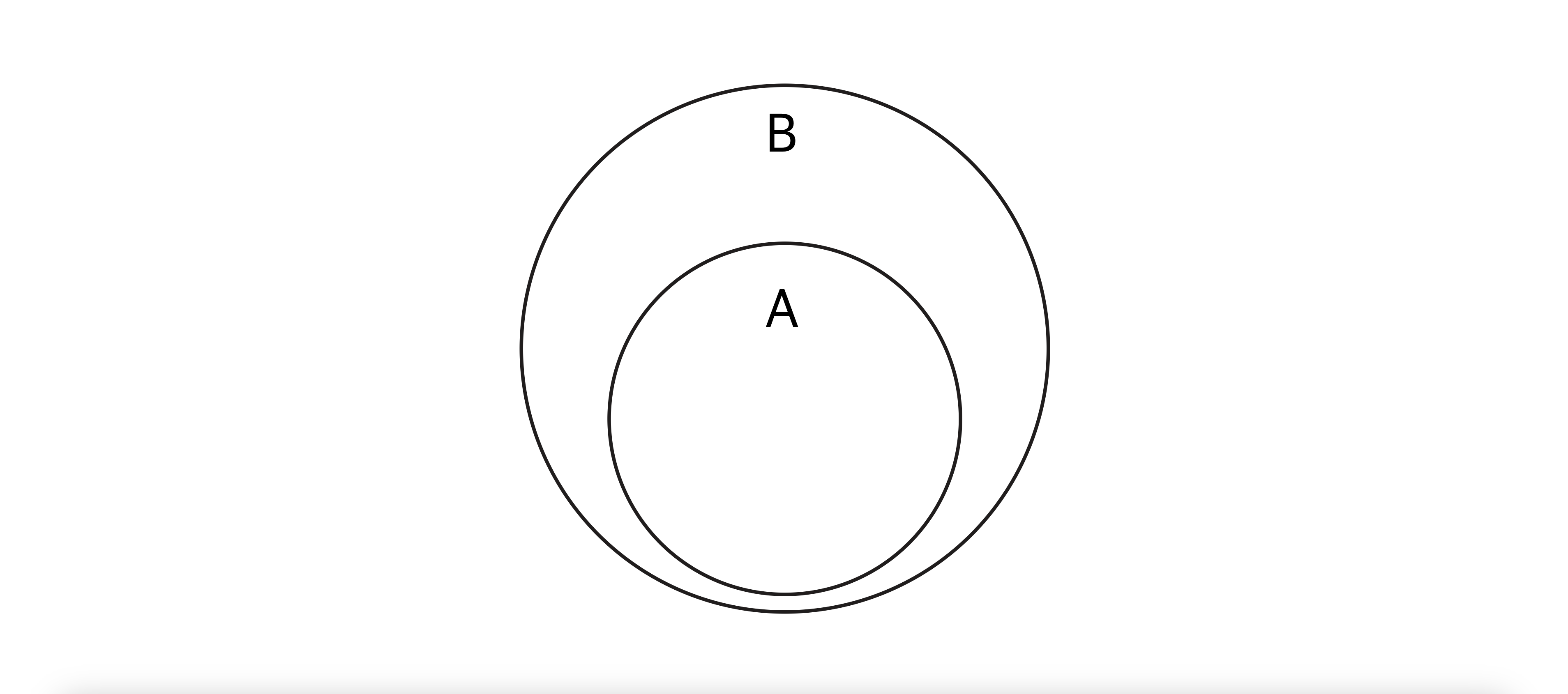
- 설명 : A Set의 모든 요소를 B Set이 포함하는지 여부 (A가 B의 부분 집합인지 여부)
- 반환값 : Boolean
- 수학적 표기 : 𝐴⊆𝐵 — B는 A의 모든 요소를 가짐
- 참고 링크 : MDN
// fours는 evens의 부분 집합
const fours = new Set([4, 8, 12, 16]);
const evens = new Set([2, 4, 6, 8, 10, 12, 14, 16, 18]);
console.log(fours.isSubsetOf(evens)); // true
// odds엔 2가 없으므로 primes는 odds의 부분 집합이 아님
const primes = new Set([2, 3, 5, 7, 11, 13, 17, 19]);
const odds = new Set([3, 5, 7, 9, 11, 13, 15, 17, 19]);
console.log(primes.isSubsetOf(odds)); // false
// A, B 집합이 동일하다면(등가 집합) 서로의 부분 집합
const set1 = new Set([1, 2, 3]);
const set2 = new Set([1, 2, 3]);
console.log(set1.isSubsetOf(set2)); // true
console.log(set2.isSubsetOf(set1)); // true
A.isSupersetOf(B) | 상위 집합
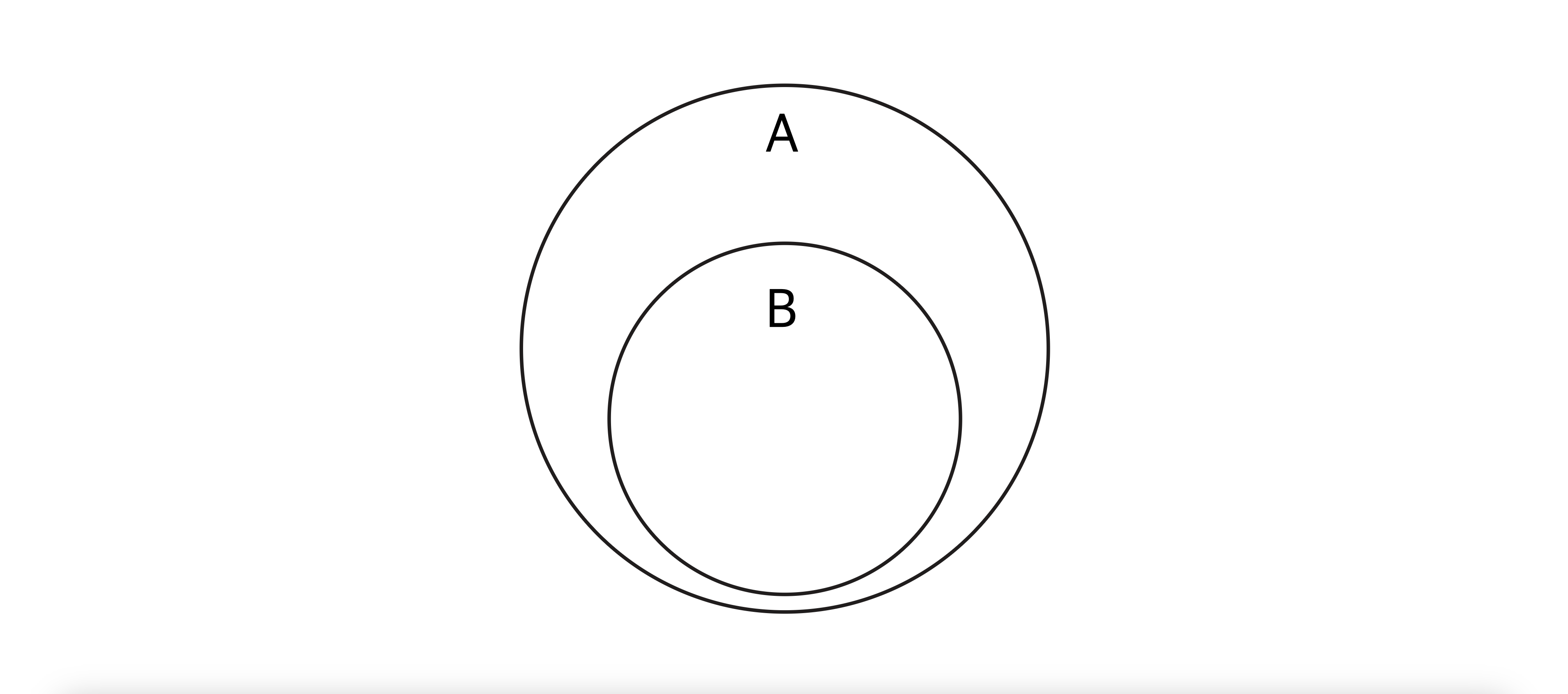
- 설명 : A Set이 B Set의 모든 요소를 포함하는지 여부 (A가 B의 상위 집합인지 여부)
- 반환값 : Boolean
- 수학적 표기 : 𝐴⊇𝐵 — A는 B의 모든 요소를 가짐
- 참고 링크 : MDN
// evens는 fours의 상위 집합
const evens = new Set([2, 4, 6, 8, 10, 12, 14, 16, 18]);
const fours = new Set([4, 8, 12, 16]);
console.log(evens.isSupersetOf(fours)); // true
// primes엔 15가 없으므로 primes는 odds의 상위 집합이 아님
const primes = new Set([2, 3, 5, 7, 11, 13, 17, 19]);
const odds = new Set([3, 5, 7, 9, 11, 13, 15, 17, 19]);
console.log(odds.isSupersetOf(primes)); // false
// A, B 집합이 동일하다면(등가 집합) 서로의 상위 집합
const set1 = new Set([1, 2, 3]);
const set2 = new Set([1, 2, 3]);
console.log(set1.isSupersetOf(set2)); // true
console.log(set2.isSupersetOf(set1)); // true
A.isDisjointFrom(B) | 서로소
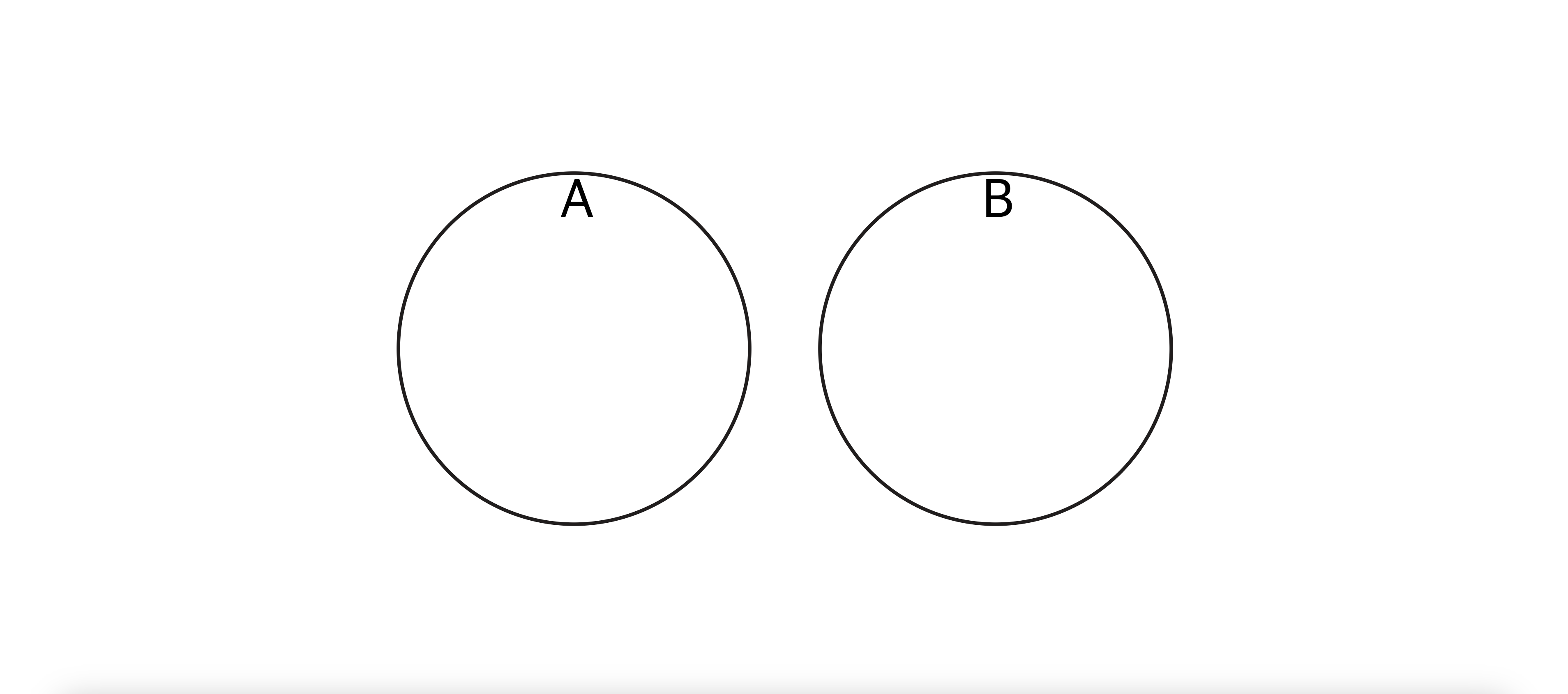
- 설명 : 두 Set이 공통 요소를 가지지 않는지 여부 (서로소 여부)
- 반환값 : Boolean
- 수학적 표기 : 𝐴∩𝐵=∅ — A, B 공통 요소 없음
- 참고 링크 : MDN
// primes, squares 공통 요소가 없으므로 서로소
const primes = new Set([2, 3, 5, 7, 11, 13, 17, 19]);
const squares = new Set([1, 4, 9, 16]);
console.log(primes.isDisjointFrom(squares)); // true
// 4, 9, 16 공통 요소를 가지므로 서로소 아님
const composites = new Set([4, 6, 8, 9, 10, 12, 14, 15, 16, 18]);
const squares = new Set([1, 4, 9, 16]);
console.log(composites.isDisjointFrom(squares)); // false
레퍼런스
New JavaScript Set methods | MDN Blog
New JavaScript Set methods are landing across browsers. Learn about sets, how you can use these methods to compare different sets, create new sets with specific properties, and more.
developer.mozilla.org
글 수정사항은 노션 페이지에 가장 빠르게 반영됩니다. 링크를 참고해 주세요
반응형
'🪄 Programming' 카테고리의 다른 글
| [JS] 자바스크립트 정규식으로 천 단위 구분자 추가하기 (단어 경계, 전후방탐색) (0) | 2024.07.18 |
|---|---|
| [JS] 자바스크립트 reduce() 메서드 활용 예시 모음 (0) | 2024.07.07 |
| [Git] RSS 글 발행 시(티스토리 등) GitHub 자동 커밋 방법 (1) | 2024.07.03 |
| [DevTools] ESLint 9 Flat Config + Prettier 설정 (TypeScript, React) (7) | 2024.06.30 |
| [DevTools] nvm보다 40배 빠른 노드 버전 관리 도구 — fnm (0) | 2024.06.18 |
댓글
이 글 공유하기
다른 글
-
[JS] 자바스크립트 정규식으로 천 단위 구분자 추가하기 (단어 경계, 전후방탐색)
[JS] 자바스크립트 정규식으로 천 단위 구분자 추가하기 (단어 경계, 전후방탐색)
2024.07.18 -
[JS] 자바스크립트 reduce() 메서드 활용 예시 모음
[JS] 자바스크립트 reduce() 메서드 활용 예시 모음
2024.07.07 -
[Git] RSS 글 발행 시(티스토리 등) GitHub 자동 커밋 방법
[Git] RSS 글 발행 시(티스토리 등) GitHub 자동 커밋 방법
2024.07.03 -
[DevTools] ESLint 9 Flat Config + Prettier 설정 (TypeScript, React)
[DevTools] ESLint 9 Flat Config + Prettier 설정 (TypeScript, React)
2024.06.30