[Algorithm] 정렬 알고리즘 기본 (버블/선택/삽입)
💡 예시의 모든 input은 [10, 7, 9, 5, 1]로 통일. 버블 / 선택 / 삽입 정렬 모두 최악의 경우 O(n²) 시간복잡도를 갖는다. 알고리즘 성능이 좋지 않아 거의 쓰진 않지만, 적은 데이터를 정렬할 땐 유용.
버블 정렬 | Bubble Sort
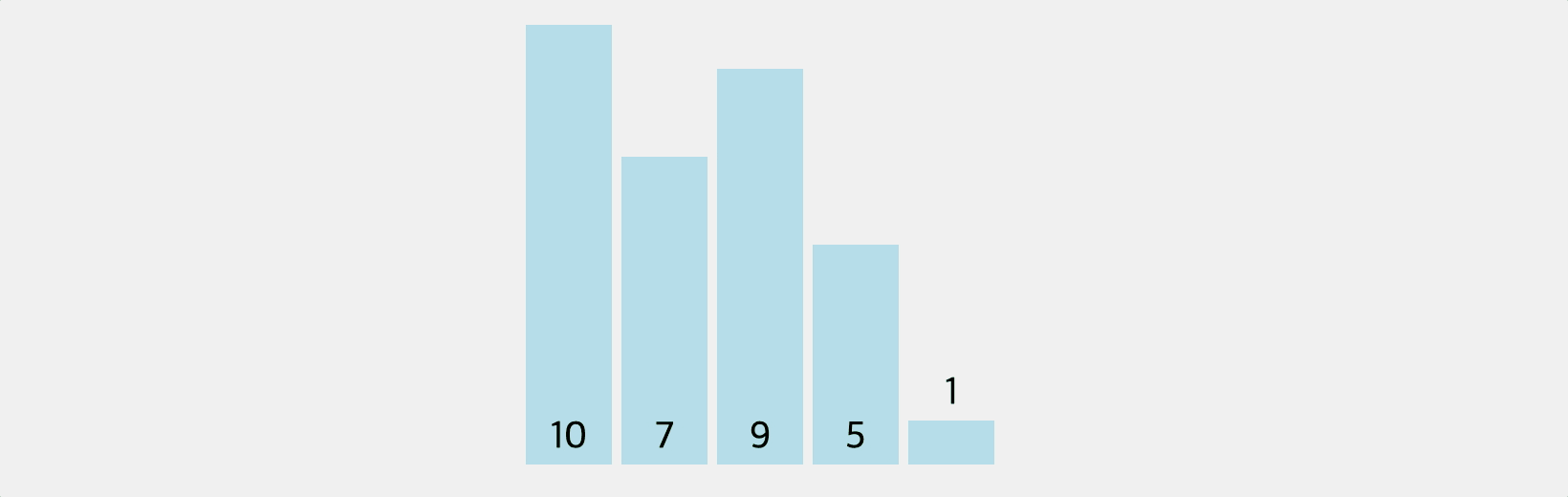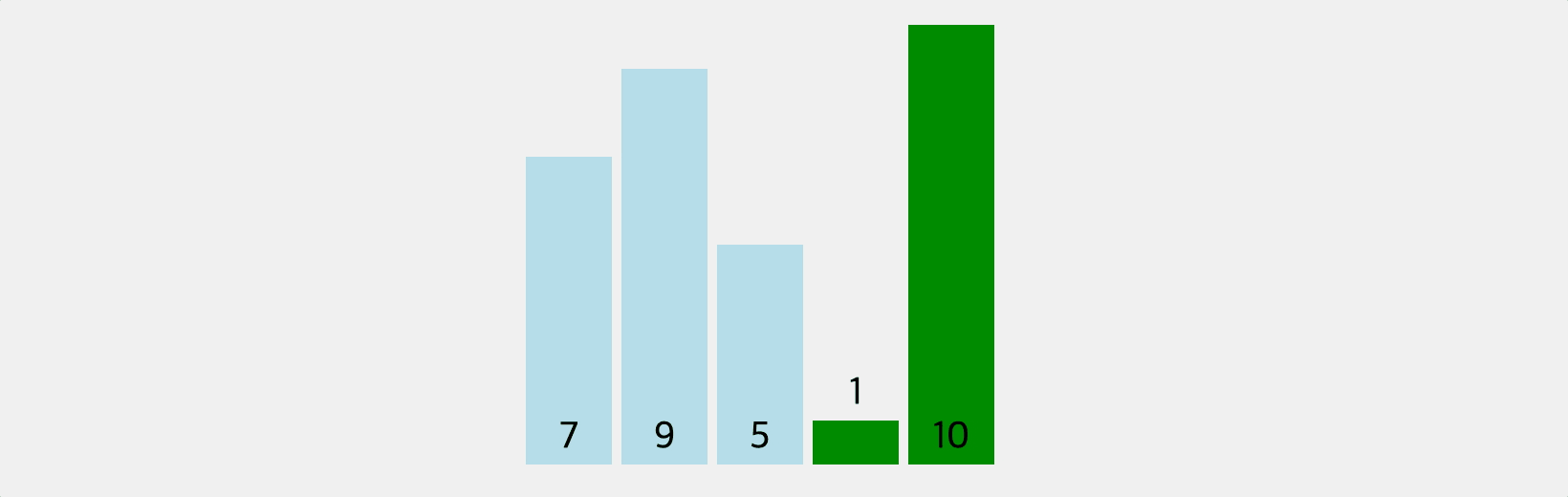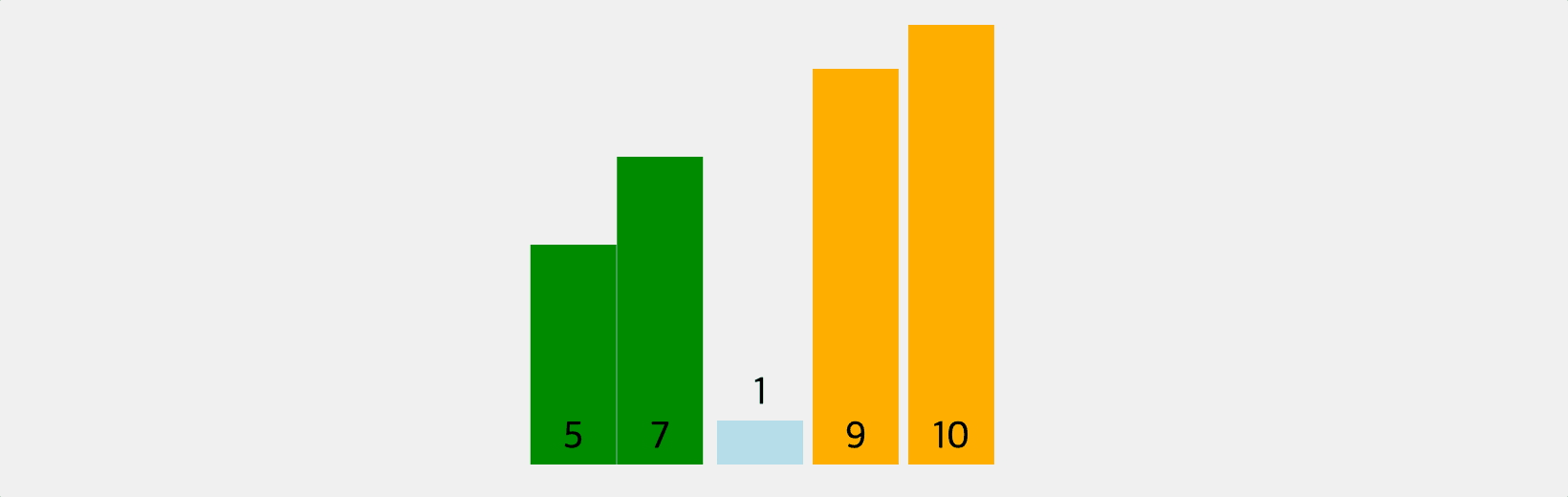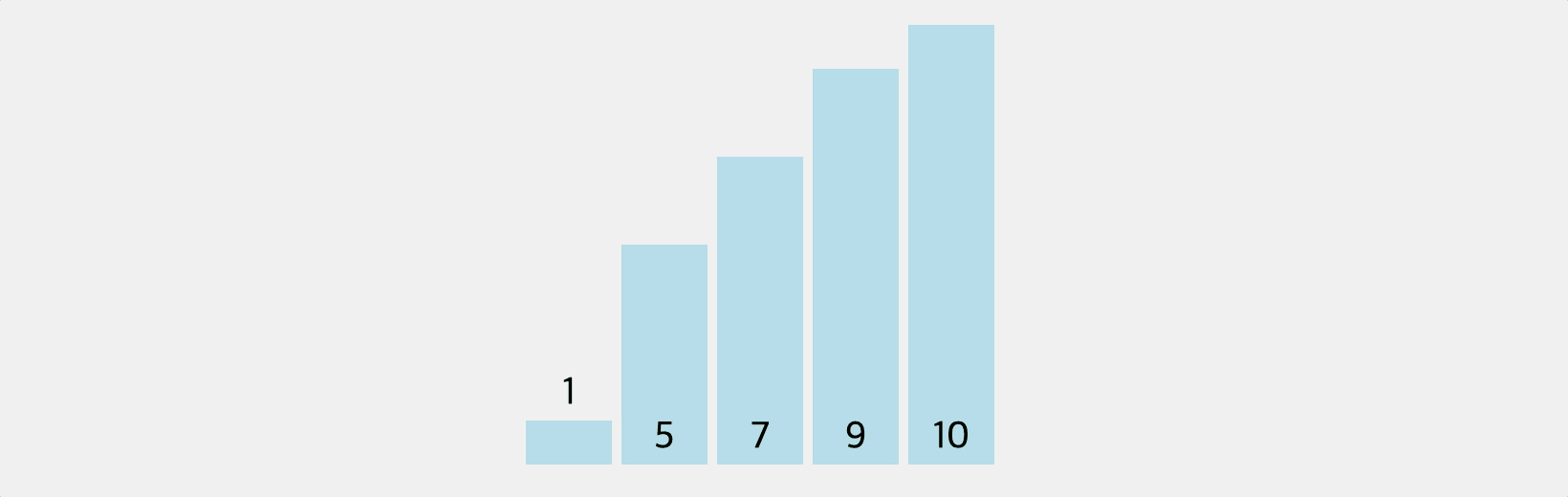
거품이 일어난 것처럼 배열의 각 요소들이 순차적으로 정렬돼서 버블 정렬이라고 부른다. 두 요소를 묶어서 비교한 후 큰 숫자를 오른쪽으로 밀어낸다. i번째 정렬을 마칠때마다 “뒤에서 i번째” 자리의 순서가 확정된다.
시간 복잡도 (삽입 정렬과 동일)
- Worst Case(정렬이 전혀 안됐을 때) :
O(n²)— 중첩 반복문을 사용하므로 - Best Case(이미 정렬됐을 때) :
O(n)
장단점 (삽입 정렬과 동일)
Stable 정렬 : 중복 데이터는 순서를 바꾸지 않는 방식(Unstable 정렬은 중복 데이터도 순서 바꿈)
In-place 정렬 : 새로운 배열 생성 없이 기존 배열만 사용하거나, 충분히 무시할만한 저장 공간만 더 사용하는 정렬 방식(Not In-place 정렬은 요소 개수에 비례하는 저장공간을 더 사용함)
- 장점 : 구현하기 쉽고,
in place알고리즘으로 메모리 절약됨.stable정렬 방식 - 단점 : 자료 개수가 많아질수록 성능이 현저하게 떨어짐. ex) 자료가 100개라면 10000번 순회
구현
i를 한 번 순회할 때마다(안쪽 for문 모두 순회) 배열의 가장 큰 요소(숫자)가 마지막 인덱스로 밀려나므로 두 번째 for문 j 조건식에서 i를 빼면 불필요한 순회를 방지할 수 있다.
const bubbleSort = (arr) => {
for (let i = 0; i < arr.length - 1; i++) {
for (let j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]; // swap
}
}
}
return arr;
};
bubbleSort([10, 7, 9, 5, 1]); // [1, 5, 7, 9, 10]i = 0, j 최대 3(arr.length - 1 - i)
========================
j = 0 : [7, 10, 9, 5, 1]
j = 1 : [7, 9, 10, 5, 1]
j = 2 : [7, 9, 5, 10, 1]
j = 3 : [7, 9, 5, 1, 10]
i = 1, j 최대 2
========================
j = 0 : [7, 9, 5, 1, 10]
j = 1 : [7, 5, 9, 1, 10]
i = 2 : [7, 5, 1, 9, 10]
i = 2, j 최대 1
========================
j = 0 : [5, 7, 1, 9, 10]
j = 1 : [5, 1, 7, 9, 10]
i = 3, j 최대 0
========================
j = 0 : [1, 5, 7, 9, 10]
배열 두 요소의 순서를 바꾸는 swap 코드는 아래와 동일하다.
if (arr[j] > arr[j + 1]) {
// [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
let temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
선택 정렬 | Selection Sort

i인덱스 위치에 올 요소를 찾는 알고리즘 ("선택"한 위치에 올 요소를 찾는 알고리즘)
선택 정렬은 i 인덱스 요소보다 작은 최소값을 찾은 후 i 인덱스 요소와 교환하는 작업을 반복하며 정렬하는 방식이다. 버블 정렬은 i번째 순회가 끝날 때마다 “뒤에서” i번째 자리의 순서가 정해지는 반면, 선택 정렬은 i번째 순회가 끝날 때마다 “앞에서” i 번째 자리의 순서가 정해진다.
시간 복잡도
- Worst Case(정렬이 전혀 안됐을 때) :
O(n²) - Best Case(이미 정렬됐을 때) :
O(n²)
장단점
- 장점 : 구현하기 쉽고
in place알고리즘으로 메모리 절약 - 단점 : 성능이 매우 떨어짐, 중복 데이터도 위치가 바뀔 수 있는
unstable정렬 방식
구현
const selectionSort = (arr) => {
for (let i = 0; i < arr.length; i++) {
let min = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
if (min !== i) {
[arr[i], arr[min]] = [arr[min], arr[i]]; // swap
}
}
return arr;
};
selectionSort([10, 7, 9, 5, 1]); // [1, 5, 7, 9, 10]i = 0 / min = 0
===============
j = 1 : min = 1
j = 2 : min = 1
j = 3 : min = 3
j = 4 : min = 4
---------------
i !== min -> [1, 7, 9, 5, 10]
i = 1 / min = 1
===============
j = 2 : min = 1
j = 3 : min = 3
j = 4 : min = 3
---------------
i !== min -> [1, 5, 9, 7, 10]
i = 2 / min = 2
===============
j = 3 : min = 3
j = 4 : min = 3
---------------
i !== min -> [1, 5, 7, 9, 10]
i = 3 / min = 3
===============
j = 4 : min = 3
---------------
i === min -> [1, 5, 7, 9, 10]
삽입 정렬 | Insertion Sort

i인덱스의 요소가 삽입될 위치를 찾는 알고리즘
삽입 정렬은 2번째(1번 인덱스) 요소부터 시작해서 왼쪽에 있는 요소와 비교한 후, 왼쪽 요소가 더 크다면 위치를 바꾸는 작업(Swap)을 반복하며 정렬하는 알고리즘이다. 버블 정렬, 선택 정렬보다 효율적이다.
1번 인덱스부터 비교 시작해서 왼쪽 값이 더 크면 Swap / 작으면 i++
---------------------------------------------------
i = 1 : 0 번 인덱스와 비교
i = 2 : 1 → 0 번 인덱스와 비교
i = 3 : 2 → 1 → 0 번 인덱스와 비교
...
시간 복잡도 (버블 정렬과 동일)
- Worst Case(정렬이 전혀 안됐을 때) :
O(n²)— 중첩 반복문을 사용하므로 - Best Case(이미 정렬됐을 때) :
O(n)
장단점 (버블 정렬과 동일)
- 장점 : 구현하기 쉽고,
in place알고리즘으로 메모리 절약됨.stable정렬 방식 - 단점 : 자료 개수가 많아질수록 성능이 현저하게 떨어짐. ex) 자료가 100개라면 10000번 순회
구현
const insertionSort = (arr) => {
for (let i = 1; i < arr.length; i++) {
let j = i;
while (j > 0 && arr[j - 1] > arr[j]) {
// arr[j] 왼쪽 요소가 더 큰지 확인
[arr[j], arr[j - 1]] = [arr[j - 1], arr[j]]; // swap
j--;
}
}
return arr;
};
insertionSort([10, 7, 9, 5, 1]); // [1, 5, 7, 9, 10]i = 1
========================
j = 1 : [7, 10, 9, 5, 1]
i = 2
========================
j = 2 : [7, 9, 10, 5, 1]
i = 3
========================
j = 3 : [7, 9, 5, 10, 1]
j = 2 : [7, 5, 9, 10, 1]
j = 1 : [5, 7, 9, 10, 1]
i = 4
========================
j = 4 : [5, 7, 9, 1, 10]
j = 3 : [5, 7, 1, 9, 10]
j = 2 : [5, 1, 7, 9, 10]
j = 1 : [1, 5, 7, 9, 10]
레퍼런스
글 수정사항은 노션 페이지에 가장 빠르게 반영됩니다. 링크를 참고해 주세요
'🪄 Programming' 카테고리의 다른 글
| [Algorithm] 퀵 정렬(Quick Sort) 알고리즘 톺아보기 (0) | 2024.05.07 |
|---|---|
| [Algorithm] 분할 정복 / 병합 정렬 알고리즘 (0) | 2024.05.07 |
| [React] 리액트 Suspense 톺아보기 (0) | 2024.05.06 |
| [Git] 알면 유용한 GitHub 단축키 / 팁 (0) | 2024.05.05 |
| [TS] 타입스크립트 제약 조건과 조건부 타입 (0) | 2024.05.05 |
댓글
이 글 공유하기
다른 글
-
[Algorithm] 퀵 정렬(Quick Sort) 알고리즘 톺아보기
[Algorithm] 퀵 정렬(Quick Sort) 알고리즘 톺아보기
2024.05.07 -
[Algorithm] 분할 정복 / 병합 정렬 알고리즘
[Algorithm] 분할 정복 / 병합 정렬 알고리즘
2024.05.07 -
[React] 리액트 Suspense 톺아보기
[React] 리액트 Suspense 톺아보기
2024.05.06 -
[Git] 알면 유용한 GitHub 단축키 / 팁
[Git] 알면 유용한 GitHub 단축키 / 팁
2024.05.05