[CS] 베지에 곡선 원리 이해하기 feat. 카스텔조 알고리즘
CSS에서 애니메이션이나 전환 효과를 제어할 때 타이밍 함수(가속도 곡선)를 사용한다. 타이밍 함수는 애니메이션이 얼마나 빠르게 또는 느리게 시작하고 끝나는지를 결정하는 수학적인 함수다. 쉽게 말해 애니메이션의 속도 변화를 제어하는 역할을 한다.
Tailwind CSS를 사용한다면 ease-in, ease-out, ease-in-out 등 미리 정의되어 있는 유틸리티 클래스를 사용해서 다양한 가속도 곡선을 적용할 수 있다.
<!--
transition-timing-function: cubic-bezier(0.4, 0, 1, 1);
transition-duration: 300ms;
-->
<button class="ease-in duration-300 ...">Button A</button>
예를 들어 ease는 부드럽게 시작해서 부드럽게 끝나고(일반적인 가속도 곡선), ease-in은 느리게 시작해서 빠르게 끝나는 효과를 줄 때 사용한다.
사실 ease, ease-in, ease-out, ease-in-out 등은 CSS에서 기본적으로 제공하는 타이밍 함수(easing function) 프리셋이다. 각 값은 아래처럼 cubic-bezier 곡선으로 미리 정의되어 있다.
ease /* cubic-bezier(0.25, 0.1, 0.25, 1) */
ease-in /* cubic-bezier(0.42, 0, 1, 1) */
ease-out /* cubic-bezier(0, 0, 0.58, 1) */
ease-in-out /* cubic-bezier(0.42, 0, 0.58, 1) */
...
베지에 곡선은 컴퓨터 그래픽스에서 부드러운 곡선을 표현하기 위해 사용하는 수학적 곡선으로, 조절점(control point)이라고 부르는 점들의 집합으로 정의된다. n개의 조절점이 주어지면 n-1차 베지에 곡선을 만들 수 있다.
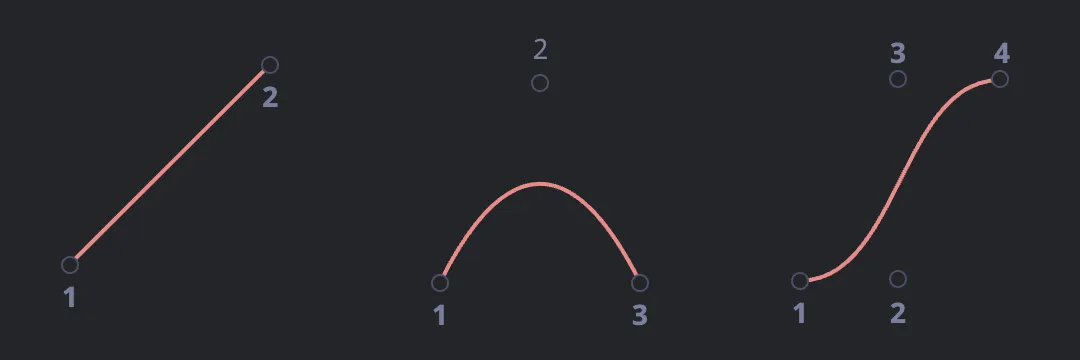
CSS에서 사용하는 cubic-bezier() 함수는 4개의 조절점(P₀, P₁, P₂, P₃)으로 구성된 3차 베지에 곡선을 기반으로 한다. 이 중 시작점(P₀)과 끝점(P₃)은 항상 (0, 0)과 (1, 1)로 고정되어 있다. 따라서 실제로는 중간에 있는 두 제어점(P₁, P₂)만 직접 설정한다.
/* cubic-bezier(P1.x, P1.y, P2.x, P2.y) 형태로 사용 */
transition: width 1s cubic-bezier(0.12, 0.83, 0.92, 1);
/* x 좌표(지속시간)는 반드시 [0, 1] 범위 내에 있어야 함 */
cubic-bezier(0.25, 0.1, 0.75, 1.0) /* ✅ */
cubic-bezier(1.5, 0.1, 0.75, 1.0) /* ❌ */
/* y 좌표(진행률)는 [0, 1] 범위를 벗어날 수 있으며, 범위를 벗어나면 바운싱 효과 생성 */
cubic-bezier(0.1, -0.6, 0.2, 2.0)
한편, 베지에 곡선은 카스텔조 알고리즘을 통해 만들 수 있다. 주어진 조절점을 선분(시작점과 끝점이 정해진 직선)으로 연결한 후, 각 선분을 동일한 비율 t로 내분(선분을 주어진 비율로 나눔; 선형 보간)하여 새로운 점들을 구하는 과정을 기반으로 한다. 두 점 사이의 선분을 특정 비율 t로 나누는 연산은 내분 혹은 선형 보간이라고 부른다.
점의 개수가 1개만 남을 때까지 선형 보간을 반복하면, 최종적으로 남은 점이 베지에 곡선 위의 좌표가 된다. 즉, 카스텔조 알고리즘은 선형 보간을 재귀적으로 적용하여 곡선의 점을 계산하는 방식이다.
글만 보면 이해하기 어려울 수도 있으니 2차 베지에 곡선부터 하나하나 만들어보자.
🔍 보간 (插值, Interpolation)
보간은 이미 알고 있는 여러 지점을 기반으로, 그 사이의 알려지지 않은 값을 추론하는 모든 과정을 가리킨다. 한자 뜻 그대로 사이(間)를 보충(補)한다는 의미. 예를 들어 $x=0$일 때 값이 $0$이고 $x=10$일 때 값이 $100$이라면, 그 사이인 $x=3$이나 $x=7$의 값을 추정하는 과정이 바로 보간이다.
🔍 선형 보간 (线性插值, Linear Interpolation)
선형 보간은 이러한 보간 기법 중 가장 대표적이고 간단한 방법. 선형 보간은 알려진 두 점을 직선으로 잇는다고 가정하고, 그 직선 위의 중간 값을 계산하는 방식이다. 줄여서 Lerp라고도 부른다. 참고로 선형은 직선 형태를 가리킨다.
2차 베지에 곡선
먼저 A, B, C 조절점 3개를 직선으로 잇는다. 그럼 AB, BC 2개의 선분이 생긴다.

각 선분을 동일한 비율 t(0 ≤ t ≤ 1)로 나눈다(내분). 예를 들어 t가 0.3이라면 A에서 B 방향으로 30% 이동한 지점 D와, B에서 C 방향으로 30% 이동한 지점 E가 만들어진다.

점 D와 E를 다시 직선으로 이어 새로운 선분 DE를 만든다.

이 선분에서 다시 t만큼 이동한 지점 F를 구한다. 점이 F 하나만 남았으므로 이 지점이 베지에 곡선의 좌표가 된다.

t 값을 0부터 1까지 조금씩 증가시키며(0.05, 0.1, …, 0.95, 1) 위 과정을 반복하면, 여러 개의 점이 생성되고, 이 점들을 순서대로 이으면 2차 베지에 곡선이 완성된다.

아래 코드펜에서 Start Animation 버튼을 클릭하면 곡선이 그려지는 과정을 직접 확인해 볼 수 있다.
See the Pen Quadratic Bezier Curves 2차 베지에 곡선 by ColorFilter (@colorfilter) on CodePen.
3차 베지에 곡선
3차 베지에 곡선은 조절점 4개로 이루어진다. 곡선을 만드는 기본 원리는 2차 베지에 곡선과 동일하지만, 조절점이 하나 늘어났기 때문에 선형 보간 과정이 한 번 더 반복된다.
먼저 A, B, C, D 조절점 4개를 직선으로 잇는다.
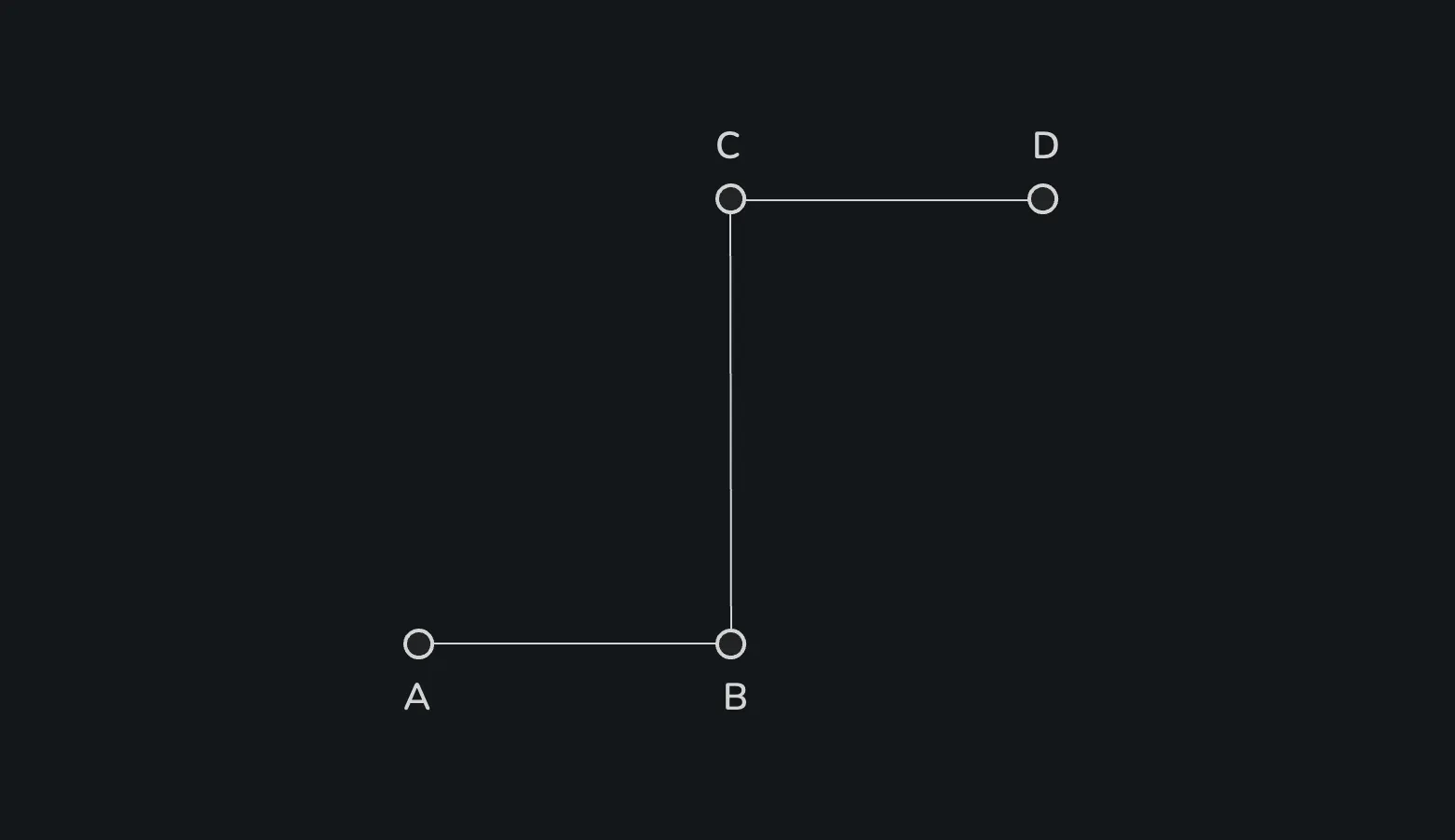
AB, BC, CD 각 선분을 동일한 비율 t로 내분한다.

내분하여 생긴 점 E, F, G를 이어 새로운 선분 EF, FG을 만든다.
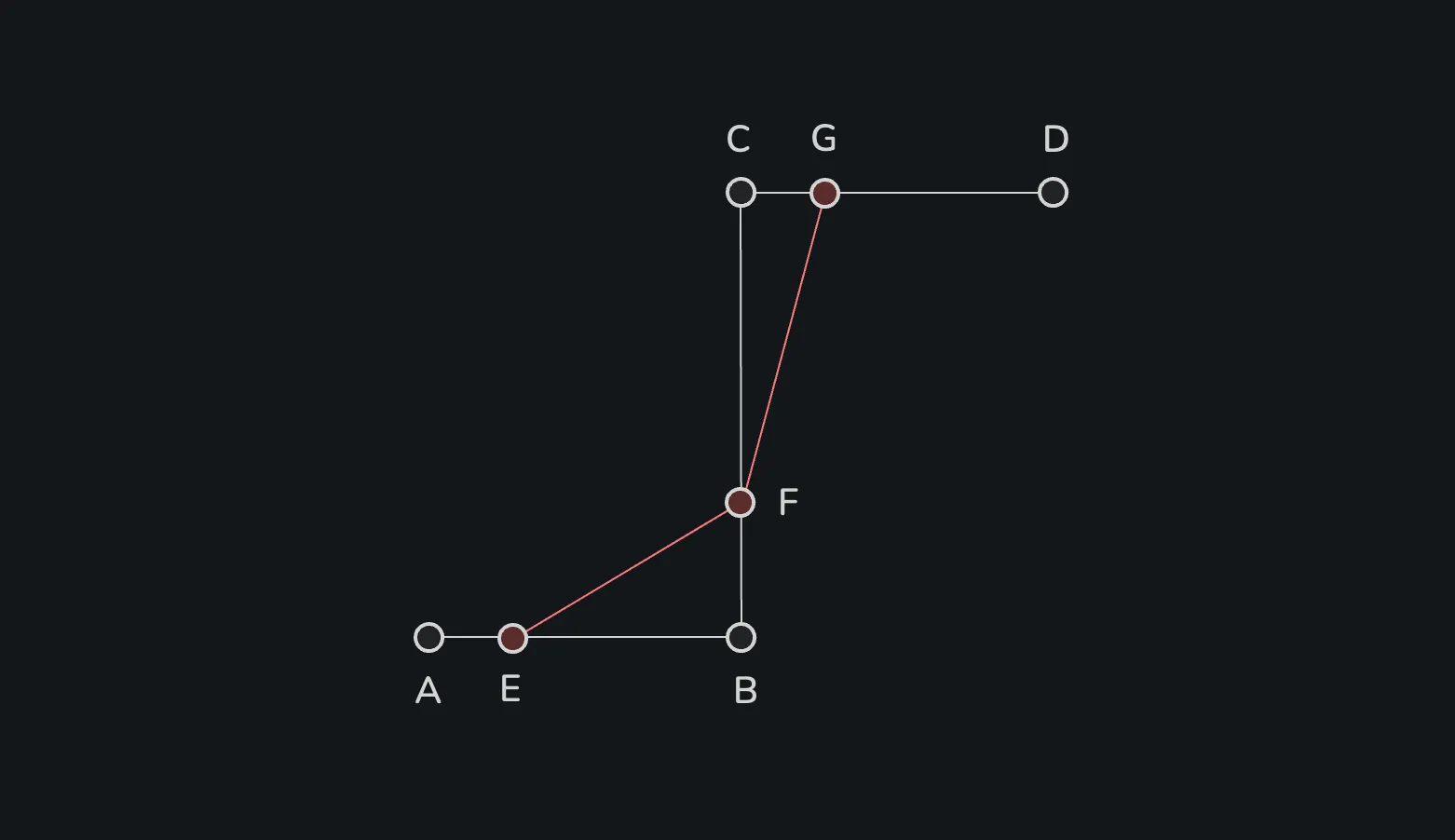
새로운 선분을 다시 t로 내분하여 점 H, I를 만든다.

내분하여 생긴 점을 직선으로 이어 선분 HI를 만든다.

선분을 다시 t만큼 내분하여 점 J를 구한다. 점이 1개만 남았으므로 이 지점이 베지어 곡선의 좌표가 된다.

3차 베지에 곡선이 만들어지는 자세한 과정은 아래 코드펜을 참고하자.
See the Pen Cubic Bezier Curves 3차 베지에 곡선 by ColorFilter (@colorfilter) on CodePen.
베지에 곡선 수학 공식 이해하기
1차 베지에 곡선 (조절점 2개)
1차 베지에 곡선(조절점 2개)은 아래 수학 공식으로 표현할 수 있다. — 선형 보간 공식
$$ P = (1-t)P_1 + tP_2 $$
$P_1$은 시작점, $P_2$는 끝점, $t$는 진행률(0 이상 1 이하, 0이면 출발 1이면 도착), $P$는 $t$에 따라 $P_1$에서 $P_2$로 이동한 위치(진행률)를 나타낸다.
예를 들어 $t = 0$일 때 $P$는 $P_1$과 정확히 일치한다.
$$ \begin{aligned} t &= 0 \\ P &= (1 - 0)P_1 + 0 \cdot P_2 \\ &= 1 \cdot P_1 + 0 \\ &= P_1 \end{aligned} $$
$t = 0.3$은 출발점 $P_1$에서 끝점 $P_2$ 방향으로 전체 거리의 30% 만큼 이동한 지점을 의미한다. 이 지점의 위치 $P$는 $P_1$과 $P_2$ 위치에 각각 가중치를 곱하여 더하는 가중 평균(weighted average) 방식으로 계산할 수 있다. 가중 평균은 위치가 더 가까운 지점에 더 큰 가중치를 부여한다. $t = 0.3$ 일 때 $P$는 $P_1$에서 30% 만큼 떨어져 있고, $P_2$에 70% 만큼 떨어져 있으므로 $P_1$에 더 가깝다. 따라서 $P_1$에 가중치를 70%, $P_2$에 가중치 30%를 적용하여 결과적으로 $P = 0.7 \cdot P_1 + 0.3 \cdot P_2$ 수식이 완성된다.
$$ \begin{aligned} t &= 0.3 \\ P &= (1 - 0.3)P_1 + 0.3 \cdot P_2 \\ &= 0.7 \cdot P_1 + 0.3 \cdot P_2 \end{aligned} $$
$t = 1$일 때 $P$는 $P_2$와 정확히 일치한다.
$$ \begin{aligned} t &= 1 \\ P &= (1 - 1)P_1 + 1 \cdot P_2 \\ &= 0 \cdot P_1 + 1 \cdot P_2 \\ &= 0 + P_2 \\ &= P_2 \end{aligned} $$
1차 베지에 곡선(선형 보간) 공식은 다음과 같이 수식을 전개하여 보다 직관적으로 나타낼 수 있다.
$$ \begin{aligned} P &= P_1-tP_1+tP_2 \\ &= P_1+tP_2-tP_1 \\ &= P_1+t(P_2-P_1) \end{aligned} $$
2차 베지에 곡선 (조절점 3개)
조절점이 3개일 때 공식은 아래와 같다. 1차 베지에 곡선의 원리를 재귀적으로 적용한 것으로 기본적인 원리는 다르지 않다. 어떤 과정을 거쳐 아래 공식이 도출되는지 하나하나 살펴보자.
$$ P = (1 - t)^2 P_1 + 2(1 - t)t P_2 + t^2 P_3 $$
먼저 2차 베지에 곡선에 필요한 3개의 조절점—시작 $P_1$, 중간 $P_2$, 끝 $P_3$—이 있다고 가정해 보자. 이 세 점을 이용해 두 개의 동적인 점을 만든다.
- $P_1$에서 $P_2$로 이동하는 점 $Q_1 = (1-t)P_1+tP_2$
- $P_2$에서 $P_3$으로 이동하는 점 $Q_2 = (1-t)P_2+tP_3$
매개변수 $t$가 0에서 1로 변함에 따라, $Q_1$은 $P_1$에서 $P_2$로, $Q_2$는 $P_2$에서 $P_3$으로 일정하게(선형적) 이동한다. 2차 베지에 곡선 위의 최종적인 점 $P$는 이렇게 움직이는 두 점 $Q_1$, $Q_2$를 다시 $t$에 대해 선형 보간하여 얻을 수 있다. 즉, $Q_1$을 시작점으로 $Q_2$를 끝점으로 갖는 또 다른 1차 베지에 곡선을 만드는 것이다.
$$ P = (1-t)Q_1 + tQ_2 $$
이제 위 공식에 $Q_1$과 $Q_2$ 정의를 각각 대입해 보자.
$$ \begin{aligned} P &= (1-t){\color{cyan}Q_1} + {\color{orange}tQ_2} \\ &= (1-t){\color{cyan}((1-t)P_1 + tP_2)} + {\color{orange}t((1-t)P_2 + tP_3)} \end{aligned} $$
분배법칙을 이용해 곱셈을 전개한다.
$$ P = {\color{cyan}(1-t)(1-t)P_1 + (1-t)tP_2} + {\color{orange}t(1-t)P_2 + t \cdot tP_3} $$
거듭제곱(²)을 사용해서 식을 정리한다.
$$ P = {\color{yellowgreen}(1-t)^2P_1} + (1-t)tP_2 + t(1-t)P_2 + {\color{yellowgreen}t^2P_3} $$
가운데 있는 2개의 $P_2$ 항은 곱의 순서만 다를 뿐 동일하므로(동류항) 하나로 합쳐준다. 그럼 2차 베지에 곡선의 공식이 완성된다.
$$ P = (1-t)^2P_1+{\color{yellowgreen}2(1-t)tP_2}+t^2P_3 $$
3차, 4차 등 더 높은 차수의 베지에 곡선도 위와 동일한 원리가 재귀적으로 적용되어 만들어진다.
참고로 각 조절점 앞에 곱해진 $(1-t)^2$, $2(1-t)t$, $t^2$ 같은 항들을 번스타인 기저 다항식(Bernstein basis polynomials) 이라고 부른다. 이러한 항들은 $t$ 값에 따라 각 조절점이 곡선 위의 점 $P$에 얼마나 큰 영향(가중치)을 미치는지 결정한다.
베지에 곡선의 기울기
아래는 다양한 베지에 곡선 예시.
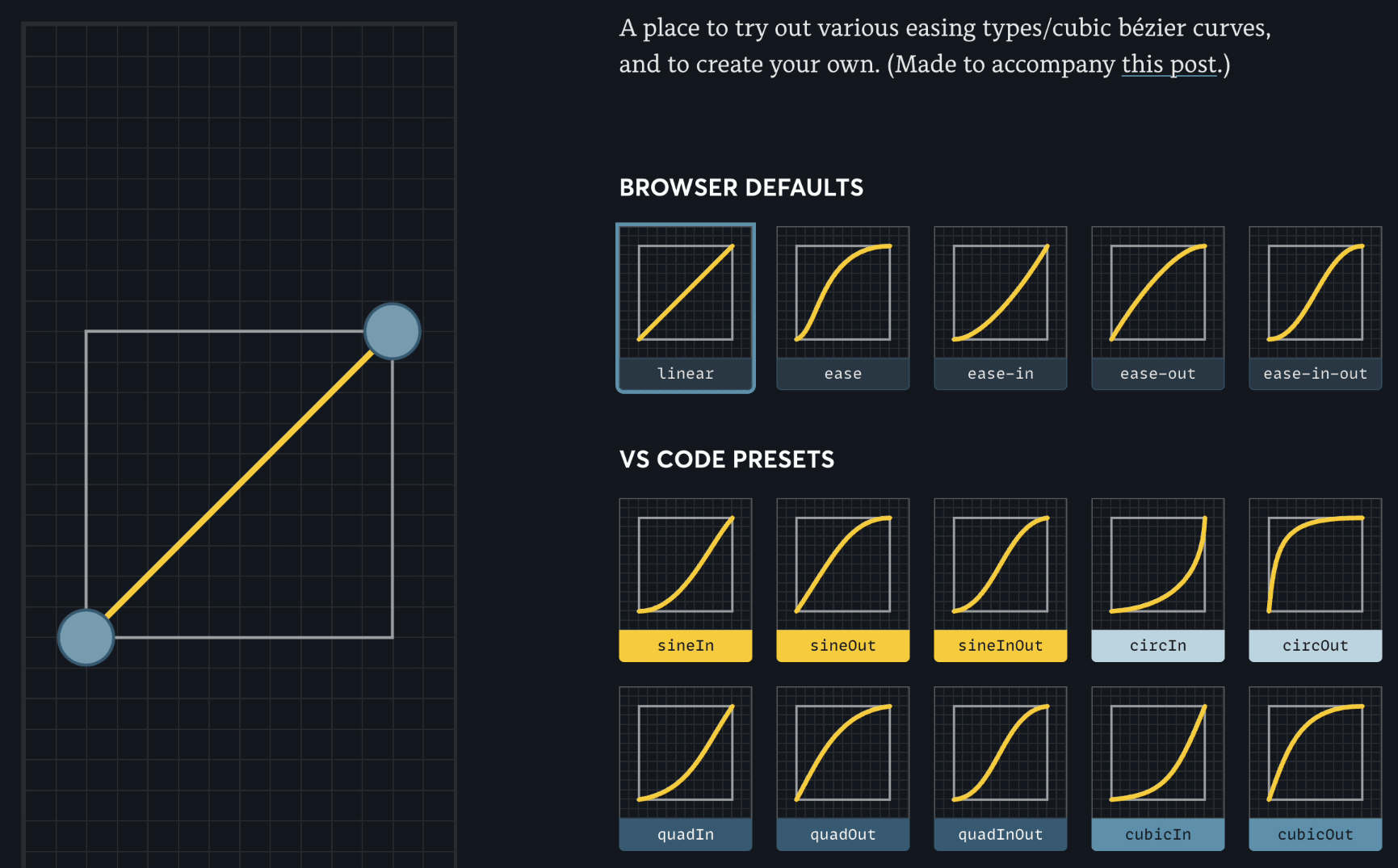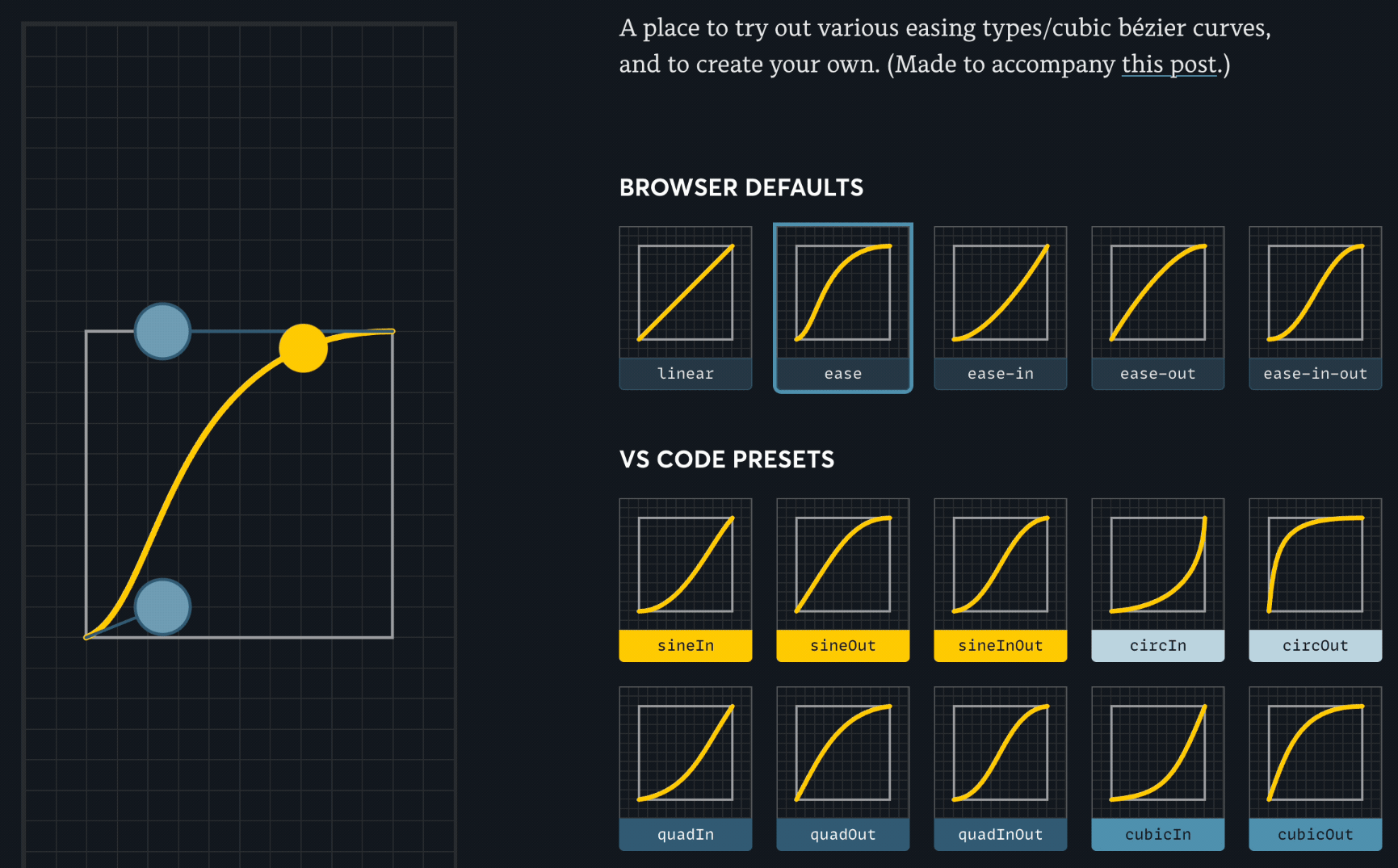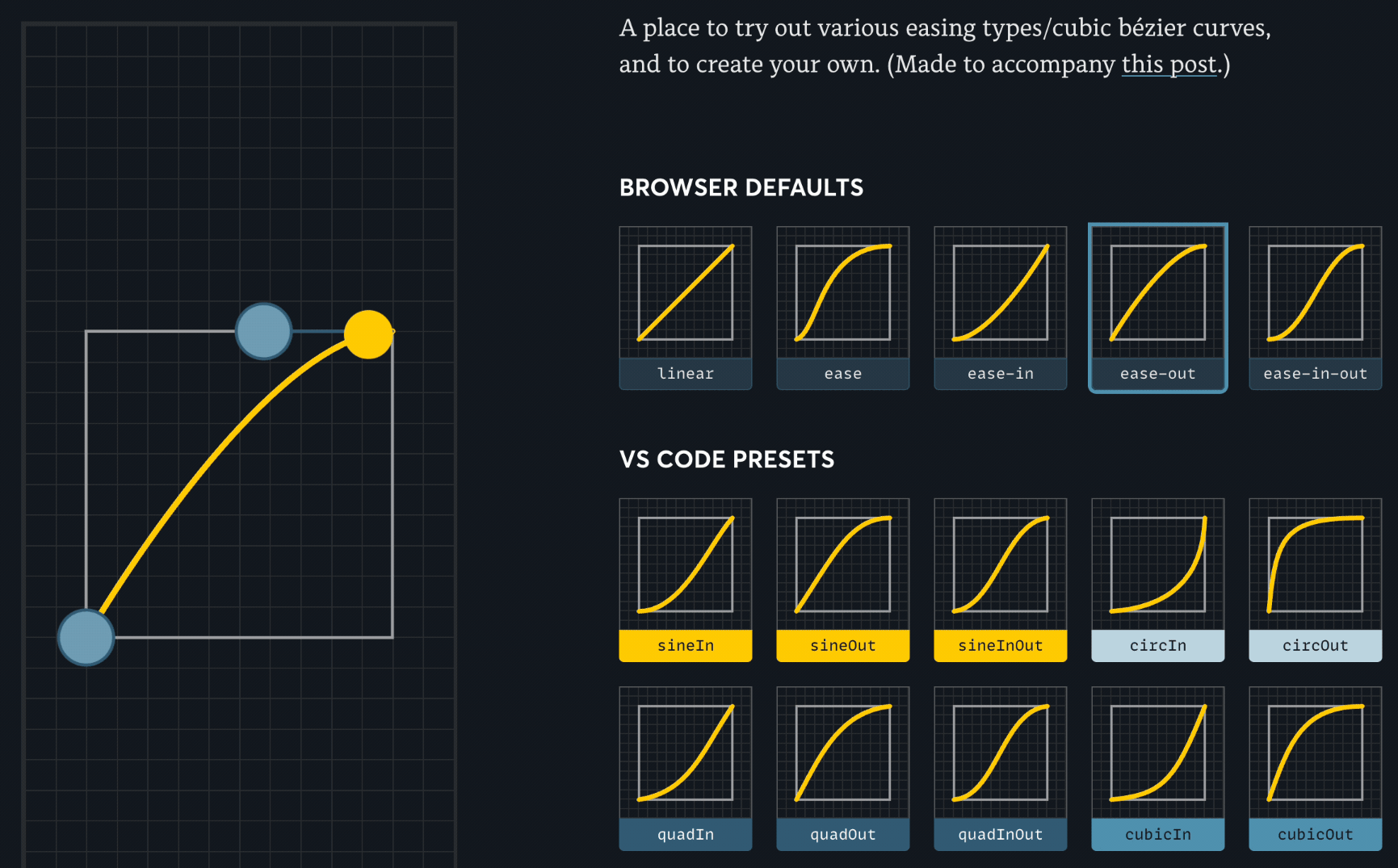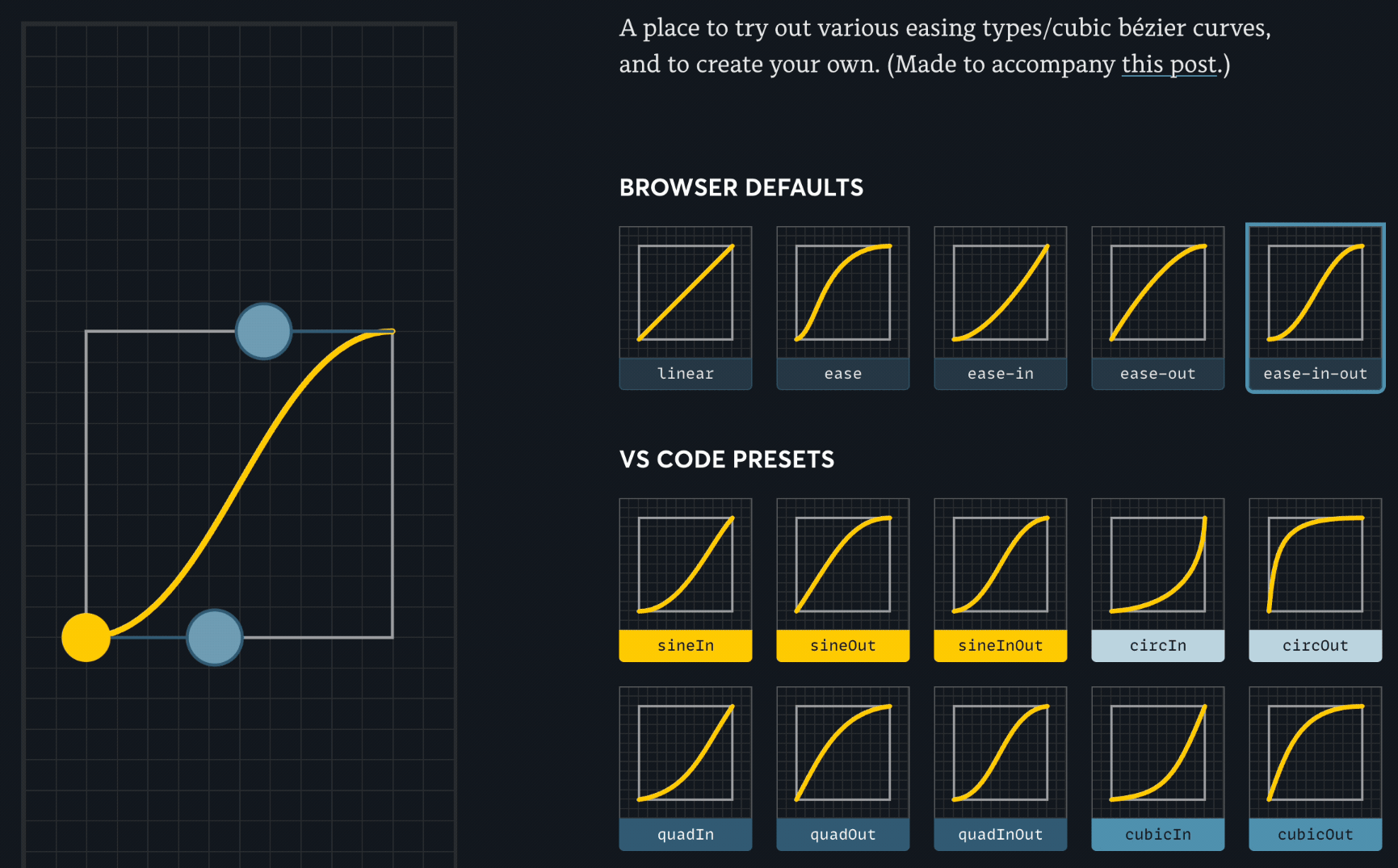
베지에 곡선 그래프에서 x축은 시간의 흐름(지속 시간), y축은 애니메이션의 진행률을 나타낸다. 이때 곡선의 기울기가 그 순간의 속도가 된다. 따라서 기울기가 가파를수록 빠르게, 완만할수록 느리게 움직이는 효과를 낼 수 있다.

x축은 애니메이션의 전체 지속시간을 1로 정규화했으므로 항상 0~1 범위로 지정해야 하지만, y축은 목표값 1을 넘어섰다가 다시 돌아오는 패턴을 활용해서 바운스 효과를 만들 수 있다.
[0 → 0.5 → 0.8] → [1.1] → [0.95 → 1.02 → 0.98] → [1.0]
가속구간 오버슈트 바운스 도달
- 가속 구간 (0 → 0.8): 기울기가 증가하면서 점점 빨라짐
- 오버슈트 (1.1): y 값이 1.1에 도달했을 때 순간적으로 속도가 0이 된 후 운동 방향 전환
- 바운스 (0.95 → 1.02 → 0.98): 목표값을 중심으로 y값이 위아래로 여러 번 출렁이는 구간
- 도달 (1.0): 목표값에 도달하여 멈추는 구간
예를 들어 cubic-bezier(0.34, 1.56, 0.64, 1) 처럼 설정하면 오버슈트 효과를 만들 수 있다. 참고로 오버슈트(Overshoot)는 목표 지점(1)을 의도적으로 넘어갔다가 다시 목표 지점으로 되돌아오는 움직임이고, 언더슈트(Undershoot)는 반대로 시작 지점(0) 보다 더 뒤로 갔다가 다시 목표 지점으로 향하는 움직임을 의미한다.
코드 및 데모
베지에 곡선 애니메이션 구현 코드(타입스크립트)는 레포지토리 링크에서 확인할 수 있다. 아래는 구현 결과를 렌더링한 화면(데모 링크). 셀렉트 박스를 눌러서 곡선의 차수(Degree)를 직접 변경할 수 있다.
레퍼런스
'🪄 Programming' 카테고리의 다른 글
| [OS] 하드 링크, 심볼릭 링크 차이점 (0) | 2025.10.19 |
|---|---|
| [JS] 두 점 사이의 거리 계산하기 (0) | 2025.07.20 |
| [JS] async 함수가 await를 만났을 때 동작 흐름 (1) | 2025.06.14 |
| [CSS] grid-row 동작 방식 살펴보기 (0) | 2025.06.03 |
| [HTTP] ETag 엔티티 태그 헤더 (0) | 2025.05.05 |
댓글
이 글 공유하기
다른 글
-
[OS] 하드 링크, 심볼릭 링크 차이점
[OS] 하드 링크, 심볼릭 링크 차이점
2025.10.19 -
[JS] 두 점 사이의 거리 계산하기
[JS] 두 점 사이의 거리 계산하기
2025.07.20 -
[JS] async 함수가 await를 만났을 때 동작 흐름
[JS] async 함수가 await를 만났을 때 동작 흐름
2025.06.14 -
[CSS] grid-row 동작 방식 살펴보기
[CSS] grid-row 동작 방식 살펴보기
2025.06.03