[CS] 컴퓨터의 실수(Real Number) 표현 - 고정 소수점, 부동 소수점, 지수 표기법, 정규화 총 정리
실수를 2진수로 변환하기
2진수는 0과 1, 두 개의 숫자만을 사용하여 정보를 표현하는 방법이다. 컴퓨터는 내부적으로 2진수를 이용하여 데이터를 저장하고 처리한다. 비트(bit)는 binary digit의 줄임말로 이진 숫자 체계의 기본 단위이다. 각 비트는 0 또는 1의 값을 가질 수 있다.
정수
일상생활에서 사용하는 10진수 숫자 100을 2진수로 변환하려면, 몫이 0이 될 때까지 2로 나누고, 마지막에 나온 나머지부터(역순으로) 나열하면 된다.

유한 소수
정수는 위처럼 간단하게 변환할 수 있지만, 0.5, 0.33 같은 실수를 변환하려면 더 복잡한 과정이 필요하다.
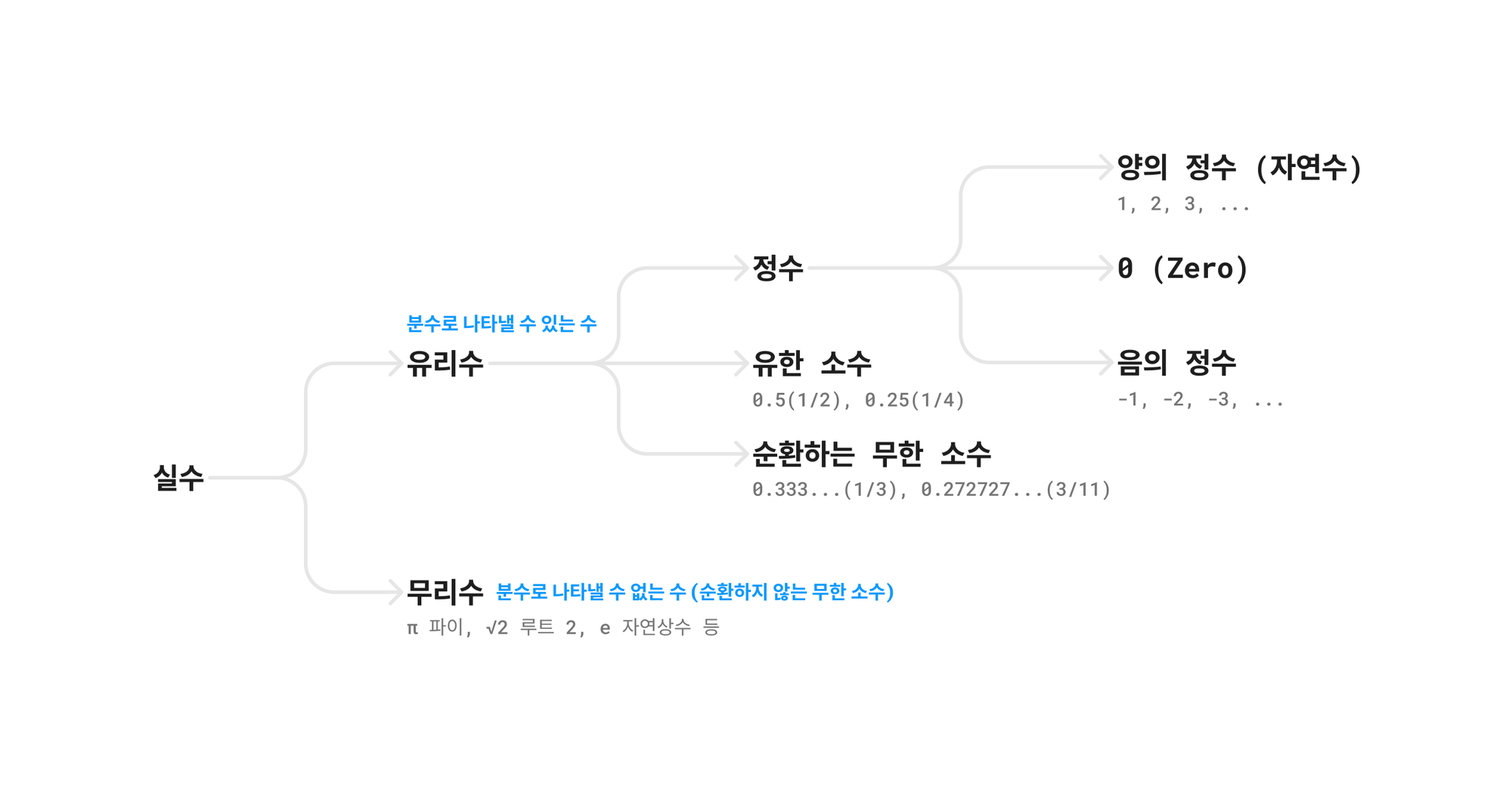
예를 들어 10진수 68.625를 2진수로 변환하려면 숫자를 정수부와 소수부로 분리해야 한다. 10진수 68.625의 정수부는 68, 소수부는 0.625다. 정수부는 위와 동일한 방법으로 2진수로 변환할 수 있다.

소수부를 2진수로 변환하려면 2를 곱한 후 그 결과의 정수부를 기록하고, 소수부만 가져와서 다시 2를 곱해준다. 이 과정을 계산 결과가 1이 되거나(소수부 0), 똑같은 소수부가 나올 때까지 반복하고, 기록된 정수부를 처음부터 나열하면 된다.

이제 정수부와 소수부를 합치면 10진수 68.625에 대한 2진수 변환이 완료된다.

무한 소수
0.3 같은 소수를 2진수로 변환해 보면 $0.01001100110011001\cdots$ 이렇게 일정한 패턴(1001)이 계속 반복되는데 이러한 숫자는 무한히 반복되는 이진 소수라고 부른다. 이러한 무한 소수는 소수점 아래의 숫자가 끝없이 반복되므로 정확한 2진수 표현을 갖지 않는다. 컴퓨터는 이러한 유형의 소수를 정확하게 표현하거나 계산할 수 없기 때문에 근삿값을 사용해서 표현한다.

이진 소수 → 십진수 변환
소수점을 가지는 이진수를 십진수로 변환하려면 소수점 이전과 이후를 분리해서 계산한 뒤 두 값을 합치면 된다. 소수점 이전은 오른쪽부터 각 이진 자릿수에 해당하는 2의 거듭제곱을($2^{n}$) 곱하고 그 결과를 모두 더한다. 소수점 이후는 왼쪽부터 각 이진 자릿수에 해당하는 2의 음의 거듭제곱을($2^{-n}$) 곱하고 그 결과를 모두 더하면 된다.
각 자리수를 나타내는 n은 소수점 왼쪽은 0부터, 소수점 오른쪽은 -1부터 시작한다. 참고로 $2^{-n}$ 같은 음의 지수는 역수 $\frac{1}{2^{n}}$가 된다. 역수는 어떤 수를 곱하여 1을 만들 수 있는 수다(예를 들어 0.125에 8을 곱하면 1이 되므로 0.125는 8의 역수다 $8 \times \frac{1}{8}=1$).
$$ \frac{1}{2^{3}} = \frac{2^{0}}{2^{3}}=2^{-3} $$
❶ 곱셈 법칙 (Multiplication Rule) : 같은 밑의 지수를 곱할 땐 지수를 더한다.
$$\begin{align*} a^m \times a^n &= a^{m+n} \\ 2^2 \times 2^3 &= (2 \times 2) \times (2 \times 2 \times 2) \\ &= 2^{2+3} \end{align*}$$
❷ 나눗셈 법칙 (Division Rule) : 같은 밑의 지수를 나눌 땐 위의 지수에서 아래 지수를 뺀다.
$$\begin{align*}a^m \div a^n &= a^{m-n} \\2^5 \div 2^3 &= (2 \times 2 \times 2 \times 2 \times 2) \div (2 \times 2 \times 2) \\&= 2^{5-3}\end{align*}$$
❸ 거듭제곱의 곱셈 법칙 (Power of a Product Rule) : 두 수의 곱을 거듭제곱할 땐 각 수를 따로 거듭제곱하여 곱할 수 있다.
$$\begin{align*}(ab)^n &= a^n \times b^n \\(2 \times 3)^3 &= (2 \times 3) \times (2 \times 3) \times (2 \times 3) \\&= 2^3 \times 3^3\end{align*}$$
❹ 거듭제곱의 거듭제곱 법칙 (Power of a Power Rule) : 거듭제곱을 다시 거듭제곱할 땐 지수를 곱한다.
$$\begin{align*}(a^m)^n &= a^{mn} \\(2^2)^3 &= 2^2 \times 2^2 \times 2^2 \\&= 2^{2 \times 3}\end{align*}$$

컴퓨터에서 실수 표현
컴퓨터가 실수를 표현하는 방식은 대표적으로 ❶고정 소수점(Fixed-Point Number Representation) 방식과 ❷부동 소수점(Floating-Point Number Representation) 방식으로 나눌 수 있다.
고정 소수점 방식 Fixed-Point
고정 소수점 방식은 이름에서 알 수 있듯 소수점의 위치를 고정시키는 방법으로, 정수부와 소수부에 할당되는 비트의 수가 정해져 있다. 이는 정수와 소수의 표현 범위가 미리 지정되어 있음을 의미한다. 이 특성으로 인해 아주 작거나 큰 수의 표현에는 제약이 따르며, 필요하지 않은 공간까지 비트 할당이 이루어져 메모리 낭비가 발생할 수 있다.
고정 소수점 방식에서 정수와 소수의 비트 수는 시스템이나 어플리케이션 요구사항에 따라 달라질 수 있다. 예를 들어, 32비트 시스템에서는 처음 1비트를 부호로 사용하고, 나머지 31비트를 정수부와 소수부로 나눠서 사용한다.
💡 32비트 시스템은 CPU가 32비트 단위로 데이터를 처리하고 메모리 주소를 할당하는 방식을 의미한다. 참고로 32비트 시스템은 2^32개의 유일한 메모리 주소를 가질 수 있다. 이는 최대 4GB의 메모리 주소 공간을 의미한다.

- 처음 1비트 : 부호(sign). 양수는 0, 음수는 1
- 다음 15비트 : 정수부(integer part, 整数)
- 다음 16비트 : 소수부(fractional part, 小数)
10진수 68.625를 32비트 고정 소수점으로 표현하면 아래와 같다. 10진수를 2진수로 변환한 결괏값을 각각 정수부와 소수부에 넣은 후, 남은 부분을 0으로 채우면 된다

이처럼 고정 소수점 방식은 표현 방법이 단순하고 속도가 빠르지만 정수부와 소수부에 사용하는 비트가 고정되어 있기 때문에 큰 실수를 표현하기 어려운 단점이 있어 특별한 경우를 제외하곤 잘 쓰이지 않는다.
부동 소수점 방식 Floating-Point
부동(浮动) 소수점 방식은 소수점의 위치를 유동적으로 조절하여 실수를 표현하는 방법이다. 이 방식은 고정 소수점 방식과 달리 실수의 정밀도와 범위를 유연하게 조절할 수 있어 다양한 크기의 수를 표현할 수 있다. 대부분의 시스템에선 부동 소수점 방식을 사용하고 있다.
부동 소수점 방식에선 숫자를 가수부(mantissa; 尾数)와 지수부(exponent; 指数) 두 부분으로 나누어 표현한다. 가수부에는 유효 숫자를 나타내는 비트가 들어가고, 지수부에는 소수점의 위치를 나타내는 지수가 들어간다.
💡 스케일 팩터(Scale Factor)는 어떤 값이나 데이터를 확대/축소하기 위해 사용하는 수치로 부동 소수점에선 지수부가 이 역할을 수행한다. 이를 통해 다양한 크기의 수를 표현할 수 있다.
부동 소수점 방식은 제한된 메모리 공간 내에서 더 넓은 수의 범위를 표현할 수 있게 해 주지만, 여전히 유한한 비트 수로 인해 정확도에 한계가 존재했다. 미국전기전자학회(IEEE)는 이 문제를 해결하기 위해 IEEE 754 표준을 제정하여 부동 소수점 연산의 효율성을 높이고 정밀도를 향상시켰다. IEEE 754 표준에선 아래 네 가지 단계를 거쳐 실수를 부동 소수점 방식으로 변환한다.
- 2진수 정규화(normalize)
소수점을 왼쪽으로 이동시켜 가수부가 1로 시작하도록 만든다 - 부호(sign) 표기
첫 번째 비트에 부호를 표기한다. 양수는 0, 음수는 1로 표기한다 - 지수부(exponent) 표기
다음 8비트에 정규화 과정에서 얻은 지수에 bias를 더한 값을 표기한다 - 가수부(mantissa) 표기
다음 23비트에 소수부를 값으로 표기한다
IEEE 754 부동 소수점 표준은 32비트 단정도(기본 정밀도, Single-Precision)와 64비트 배정도(2배 정밀도, Double-Precision) 이 두 가지를 가장 많이 사용한다.
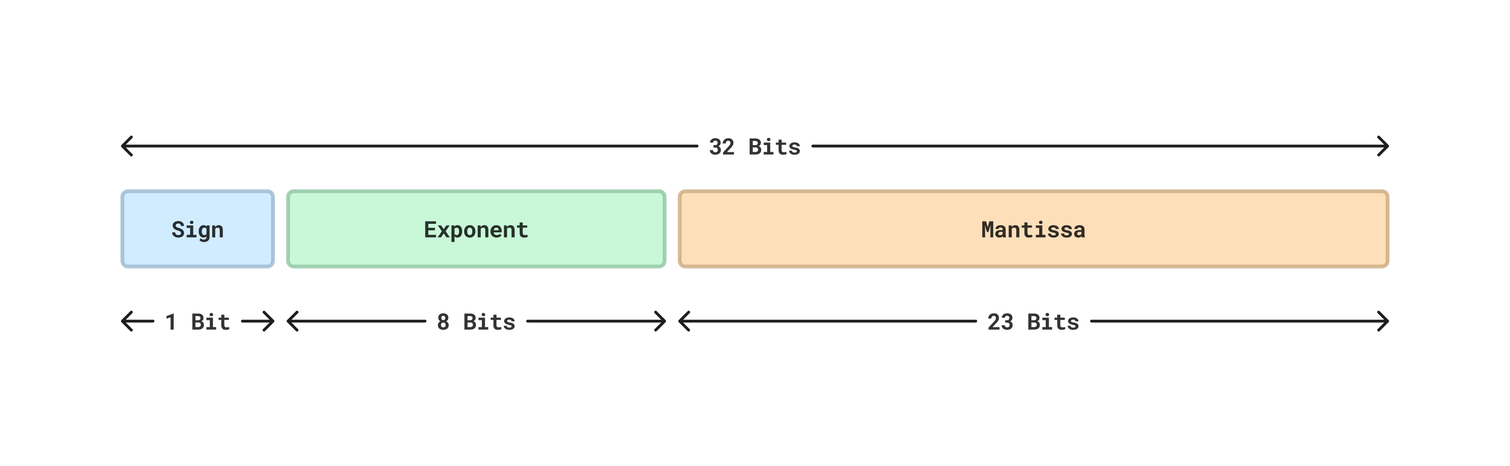

고정 소수점 방식은 일반적으로 정수부 15비트와 소수부 16비트로 구성되지만, 부동 소수점 방식은 23비트의 가수부로 실수를 표현한다. 즉, 부동 소수점은 가수부만으로 실수 표현을 할 수 있기 때문에 저장 효율이 더 높고, 고정 소수점이 가진 메모리 낭비 문제를 해결할 수 있다.
지수표기법 Exponential Notation
💡 부동 소수점은 이진수 기반이지만 아래 설명은 지수표기법의 이해를 위해 10진수를 사용했다.
부동 소수점 방식은 숫자를 가수부와 지수부 두 부분으로 나눠서 표현한다고 했다. 이를 지수표기법이라고 부르는데 큰 수나 작은 수를 간편하게 표현하기 위한 방법이다. 지수표기법은 다음과 같은 형태를 가진다.
$$a \times 10^b$$
- 가수부(a) : 숫자의 실질적인 값을 나타낸다. 가수부는 주로 1 이상 10 미만의 수로 표현한다.
- 지수부(b) : 10의 거듭제곱으로 표현하여 숫자가 얼마나 크거나 작은 지를 나타낸다.
이와 유사하게 이진수에서 지수표기법은 다음과 같이 표현할 수 있다. 가수부(a)는 이진수로 표현되고, 지수부(b)는 소수점의 위치를 결정한다.
$$a \times 2^b$$
아래는 123.456에 대한 다양한 지수표기 예시. 소수점을 왼쪽 혹은 오른쪽으로 이동하고 이동한 횟수만큼 지수로 표현하는 방식이다. 예를 들어 소수점을 왼쪽으로 두 번 이동했다면 지수는 10²가 되고 오른쪽으로 두 번 이동했다면 지수는 10⁻²가 된다.
$$\begin{align*}123.456 &= 1.23456 \times 10^2 \\&= 12.3456 \times 10^1 \\&= 1234.56 \times 10^{-1} \\&= 12345.6 \times 10^{-2}\end{align*}$$
프로그래밍이나 계산기에선 e(exponent)를 사용해서 지수를 나타낼 수도 있다. e 뒤에 오는 숫자는 일반적으로 10진수의 거듭제곱을 나타내며, e뒤에 + 기호를 붙이거나 생략할 수 있다(크롬 콘솔에 1e1 혹은 1e+1을 입력해 보면 모두 10을 출력한다).
$$\begin{align*}1000 &= 1 \times 10^3 = 1e3 \\5000000 &= 5 \times 10^6 = 5e6 \\0.01 &= 1 \times 10^{-2} = 1e-2 \\0.000005 &= 5 \times 10^{-6} = 5e-6\end{align*}$$
정규화 Normalize
정규화는 주어진 수를 표준 형식으로 변환하는 과정을 의미한다. 주로 소수점의 위치를 조정함으로써 이뤄진다. 이진수에서 정규화는 주어진 수를 $1.f\times 2^{n}$ 형태로 표기한다. 여기서 $1.f$는 정규화된 가수(mantissa)이고, $2^n$은 지수(exponent)를 나타낸다. $f$는 소수부(fractional part)를 의미하며, 소수점 이하의 비트를 나타낸다. 이 비트들은 0과 1로 구성되어 소수점 아래 값을 표현한다.
지수 표기법과 유사해 보이지만 이진수로 변환한 뒤 소수점을 이동시켜 가수부의 맨 앞자리가 항상 1이 되도록 조정하는 점이 다르다. 이는 이진수 특성상 $1.f$ 형태로 나타낼 수 있기 때문이다.
10진수 68.625를 정규화해 보면…
- 2진수 변환 : $1000100.101$
- 소수점 이동 : 앞자리가 1이 되도록 소수점을 옮겨준다 → $1.000100101$
- 지수부 구성 : 소수점 이동 횟수(6)를 지수로 사용한다 → $2^6$
- 정규화 완성 : $1.000100101\times2^6$
지수부 Exponent
💡 숫자의 진수를 표현할 때 아래 첨자(subscript)를 사용한다. 예를 들어 127이라는 숫자가 십진수임을 나타낼 때 127 우측에 ₁₀ 아래첨자를 붙여서 127₁₀ 표기한다(127₍₁₀₎ 소괄호로 감싸서 표기할 수도 있다).
32비트 IEEE 754 표준에서 실수를 표현할 땐 지수부에 $127_{10}$ 숫자를 더한 값으로 채워야 한다. 이 127 숫자는 bias라고 부른다. 예를 들어 $68.625_{10}$의 이진법 표현에서 지수 값이 6이라면 이 값에 127을 더한 후 다시 이진수로 변환해서 지수부를 채워야 한다.
- 68.625를 이진수로 변환 : $1000100.101$
- 소수점 앞자리가 1이 되도록 소수점 이동 : $1.000100101$
- 소수점을 이동한 횟수만큼 지수로 사용 : $6$
- 획득한 지수에 bias(127) 더하기 : $127+6=133$
- 더한 값 133을 다시 이진수로 변환 : $10000101$
bias 값을 더하는 이유는 지수가 음수일 때를 대비하기 위함이다. $0.078125_{10}$를 예로 들어보자. $0.078125_{10}$의 이진수는 $0.000101$ 이고 이를 정규화하면 $1.01\times2^{-4}$가 된다. 지수는 $-4$로 음수가 나왔다.


지수부의 음수와 양수를 나타내기 위해 1비트를 부호(sign) 값으로 할당할 수 있지만, 표현할 수 있는 값의 범위가 줄어드는 단점이 있다. IEEE 754 표준에선 8비트로 음수와 양수를 모두 표현하기 위해 bias라는 값을 도입했다.
8비트 지수부는 $2^8=256$개의 숫자를 표현할 수 있는데(0~255) 이 지수부 범위의 절반 지점인 127(십진수)을 기준으로 음수와 양수를 구분하는 방법이다. 계산된 지수에 bias를 더한 값이 bias 보다 작으면 음수, bias보다 크면 양수로 판별한다.
- 0~127 구간 : 음수 (저장된 지수가 100이라면 음수이고, 실제 지수는 $100-127=-27$)
- 128~255 구간 : 양수 (저장된 지수가 130이라면 양수이고, 실제 지수는 $130-127=3$)
💡 지수값 0($00000000_{2}$)과 255($11111111_{2}$)는 특별한 값을 나타내기 위해 미리 예약되어 있다. 매우 작은 값을 표현할 땐 0을 사용하고, Infinity 혹은 NaN은 255를 사용한다.
가수부 Mantissa
가수부는 고정 소수점에서 소수부(fractional part) 같은 역할을 한다. 정규화 결과의 소수 부분(소수점 오른쪽)을 가수부 자리에 넣고 남는 자리는 0으로 채워주면 된다.
예를 들어 $68.625_{10}$의 정규화 결과가 $1.000100101_{2}\times2^6$ 이라면 소수점 오른쪽에 있는 $000100101$ 숫자를 가수부에 넣고 남은 부분은 0으로 채우면 된다.

실제 예시
$68.625_{10}$ 숫자를 32비트 IEEE 754 부동 소수점으로 표현해 보면 아래와 같다. $68.625_{10}$는 양수이므로 시작 부분인 부호 비트엔 0을 입력한다.

- 2진수 변환 : $1000100.101_{2}$
- 정규화 : $1.000100101_{2}\times2^6$
- 지수부 : $6_{10}+127_{10}(bias)=133_{10}=10000101_{2}$
- 가수부 : $000100101_{2}$
부동 소수점의 한계
32비트 고정 소수점은 정수부에 15개 비트를 할당하여 최대 $2^{15}=32768$ 개의 정수를 표현할 수 있다.
한편 32비트 부동 소수점에선 지수부에 8비트를 할당한다. 8비트를 채울 수 있는 가장 큰 수는 $11111111_{2}$ 이지만, 이는 무한대를 나타내는 미리 예약된 값이므로 실제 최댓값은 $11111110_{2}$($254_{10}$)이다. 여기엔 바이어스(bias) $127_{10}$이 포함되어 있으므로 이 값을 빼고 사용할 수 있는 최대 지수는 $254-127=127$이 된다. 따라서 32비트 부동 소수점에서 표현할 수 있는 가장 큰 수의 정규화된 형태는 $1.f\times2^{127}$이다. 고정 소수점과 비교하면 훨씬 넓은 범위의 수를 표현할 수 있음을 의미한다.
하지만 부동 소수점은 실수 연산의 정확도를 보장하지 않는 단점이 있다. 고정 소수점에선 소수점의 위치가 변경되지 않기 때문에 소수점 이하의 정밀도가 일정하게 유지되지만, 표현할 수 있는 수의 범위가 한정되어 있다. 반면, 부동 소수점은 소수점의 위치를 유동적으로 조정함으로써 더 넓은 범위의 수를 표현할 수 있지만, 가수부와 지수부에 할당된 비트 수의 제한으로 정밀도에 제약이 생긴다.
예를 들어 십진수 0.3을 이진수로 변환하면 $0.01001100110011001\cdots$ 과 같이 1001이 무한 반복되는 이진 소수가 된다. 컴퓨터는 이러한 무한 소수를 표현할 수 없기 때문에 가수부 마지막 비트 이후의 값을 반올림하거나 절삭(버림) 처리한다. 결과적으로 실제 컴퓨터에 저장되는 값은 0.3이 아닌 근삿값이 되는 것이다.
💡 Python의 round 함수는 Round to Nearest, Ties to Even 방식을 채택해서 2.5는 2로, 3.5는 4로 반올림된다. Javascript의 round 함수는 Round to Nearest, Ties to Away 방식으로 2.5는 3으로, 3.5는 4로 반올림된다. 이는 우리가 일상에서 사용하는 사사오입(四舍五入) 방식과 동일하다.
IEEE 754 표준에선 제한된 비트로 생략되는 값을 처리하기 위해 5가지 방법을 정의했는데, 그중 짝수로 반올림(Round to Nearest, Ties to Even; 뱅크형 반올림)을 가장 많이 사용한다. 반올림할 자리의 수가 5이고(중간값), 그 뒤에 어떤 숫자도 오지 않거나 모두 0일 때, 앞자리 숫자가 짝수면 내림하고 홀수면 올림하는 방식이다(가장 가까운 짝수로 반올림). 아래 예시의 마지막 소수점을 반올림한다면…
- 4.5 → 4 : 반올림할 자리의 수가 5이고, 그 앞의 숫자(4)가 짝수이므로 내림
- 5.4 → 5 : 반올림할 자리의 수가 4이므로 일반적인 반올림 규칙에 따라 내림
- 0.125 → 0.12 : 반올림할 자리의 수가 5이고, 그 앞의 숫자(2)가 짝수이므로 내림
0.1 + 0.2
근삿값 계산해 보기
0.1 + 0.2; // 0.30000000000000004
0.1 + 0.2 === 0.3; // false
자바스크립트의 모든 숫자는 64비트 부동 소수점 형식(IEEE 754 표준)으로 표현한다. 콘솔에 0.1을 입력하면 이를 IEEE 754 표준 형식에 따라 2진수로 바꾸고 그 결과를 다시 10진수로 바꿔서 화면에 표시하는 것이다.
위에서 살펴봤듯 IEEE 754 표준은 2진수 형식을 사용하여 숫자를 표현하므로 일부 숫자는 정확하게 표현할 수 없다. 예를 들어 0.1과 0.2를 2진수로 변환해 보면 둘 다 소수점이 무한 반복되므로 정확한 2진수로 표현할 수 없는 숫자다. 이러한 무한 소수들은 비트의 제한으로 인해 근삿값으로 저장하기 때문에 오차가 발생한다.
- 0.1과 0.2를 2진수로 변환한다
- 두 수를 부동 소수점으로 표기하기 위해 반올림 후 근삿값으로 저장한다
- 두 수의 근삿값을 합산한다
- 합산한 근삿값을 다시 10진 수로 변환한다
⚠️ 반올림은 IEEE 754 표준의 Round to Nearest, Ties to Even 방식을 적용해야 한다



0.1 + 0.2의 이진 근삿값을 다시 10진수로 변환하는 예시 ▼
// 0.1 + 0.2의 이진 표현 (2진수 문자열)
const binaryString = '0100110011001100110011001100110011001100110011001100111';
const base = 2;
const power = -55;
const parsedInt = parseInt(binaryString, base);
const result = parsedInt * Math.pow(2, power);
console.log(result); // 0.30000000000000004
🔍 Math.pow(2, -n)은 $2^{-n}$ 음의 지수이므로 이는 역수 $\frac{1}{2^{n}}$과 동일하다. 0.5로 n번 곱하는(나누기 2를 n번 반복) 계산이라고 보면 된다. 즉, 위 코드는 parseInt() 첫 번째 인자에 주어진 이진수를 십진수로 변환한 후 0.5로 곱하는 작업을 55번 수행(나누기 2를 55번 반복) 하는 것과 같다.
또한 parseInt()를 통해 10진수로 변환할 땐 소수점은 처리하지 않는다. 때문에 이진수의 소수부만 따로 분리해서 가중치를 곱하는 방식으로 계산하는 것. 예를 들어 이진수 0.101의 소수부를 10진수로 변환할 때 1번째 소수점은 $\frac{1}{2^{1}}=0.5$, 2번째 소수점은 $\frac{1}{2^{2}}=0.25$, 3번째 소수점은 $\frac{1}{2^{3}}=0.125$의 가중치를 가진다.

🔍 toString() 메서드를 이용해 특정 숫자의 이진 근삿값을 확인해 볼 수 있다.
(0.1).toString(2); // 0.000110011... -> 0.1의 이진 근사값
(0.2).toString(2); // 0.0011001100... -> 0.2의 이진 근사값
안전한 정수의 범위
64비트 IEEE 754 표준에서(배정밀도 부동소수점) 가수부(실제 데이터가 저장되는 곳)는 52비트로 이루어져 있어 $2^{52}$개의 서로 다른 정수를 표현할 수 있다. 배정밀도 가수부 필드는 $1.f$ 형태로 항상 숨겨진 비트 1을 포함하기 때문에 실질적으로 $2^{53}$까지 정수 값을 구별할 수 있다. 음수와 양수를 모두 포함하면 $-(2^{53}-1)$에서 $2^{53}-1$까지가 표현할 수 있는 정수 범위가 된다. 이 범위 내에선 정밀도 손실 없이 부동소수점 연산을 수행할 수 있다.
자바스크립트 ES6에는 안전한 정수 범위를 나타내는 상수도 제공한다. 이 범위를 벗어나는 순간 부정확한 연산 결과가 나오므로 주의하자.
console.log(Number.MAX_SAFE_INTEGER); // 9007199254740991 = 2^53 - 1
console.log(Number.MIN_SAFE_INTEGER); // -9007199254740991 = -(2^53 - 1)
🔍 $2^{53}-1$에서 1은 왜 빼는 걸까? 3비트만 사용해서 숫자를 저장한다고 가정해 보자. 3비트에서 표현할 수 있는 가장 큰 숫자는 $111_{2}$이고 10진수로 변환하면 7이 된다. $2^{3}-1$과 동일한 값이다. 4비트만 사용할 때도 마찬가지다. $1111_{2}$를 10진수로 변환하면 15인데 이는 $2^{4}-1$과 동일하다. 이처럼 n비트로 표현할 수 있는 최댓값은 항상 $2^{n} -1$ 공식으로 계산할 수 있다.
정확한 연산 결과 얻는 법
❶ 라이브러리 사용
- math.js: 수학 연산과 고급 기능이 필요할 때 적합 / 13.6k star
- decimal.js: 정밀한 소수점 연산이 중요할 때 적합 / 5.8k star
❷ Number.toFixed([digits]) 메서드 사용 — 통화(货币) 다룰 때 유용
const num = 12345.6789;
num.toFixed(); // '12346' -> 소수점 0자리까지 표시, 소수점 1번째 자리에서 반올림
num.toFixed(1); // '12345.7' -> 소수점 1자리까지 표시, 소수점 2번째 자리에서 반올림
(0.1 + 0.2).toFixed(1); // '0.3' -> 소수점 1자리까지 표시, 소수점 2번째 자리에서 반올림
- 동작 방식: 지정한 소수점 자릿수만큼 표시하고, 그 자릿수를 넘어가는 부분은 반올림
- 파라미터: 보존할 소수점 자릿수 지정(0~20). 생략 시 0으로 처리
- 자릿수 고정 기준: 소수점
- 반환 값: 문자열
❸ Number.toPrecision([precision]) 메서드 사용 — 숫자 길이 조절 시 유용
const num = 12345.6789;
num.toPrecision(); // '12345.6789' -> 파라미터 생략해서 toString()으로 작동
num.toPrecision(1); // '1e+4' -> 1×10⁴ -> 유효 숫자 1개 표시, 2번째 자리에서 반올림
num.toPrecision(6); // '12345.7' -> 유효 숫자 6개 표시, 7번째 자리에서 반올림
(0.1 + 0.2).toPrecision(1); // '0.3' -> 유효 숫자 1개 표시, 2번째 자리에서 반올림
- 동작 방식: 전체 숫자를 기준으로 지정한 길이(정밀도) 만큼 표시하고, 그 뒷자리에서 반올림
- 10 이상 숫자를 한 자리 유효 숫자로 표기할 땐 지수 표기법(예: 1e+4)을 사용해 원래 숫자 크기 유지
- ⚠️ Leading zeroes를 제외한 숫자만 유효 자릿수로 고려하므로 주의
- 🔍 예를 들어 0.0012 숫자에선 앞쪽에 있는 0은 제외하고 12만 유효한 자릿수로 취급
- 파라미터: 유효 자릿수 지정. 생략 시
toString()으로 작동 - 자릿수 고정 기준: 전체 숫자
- 반환 값: 문자열
❹ 실수에 필요한 만큼 거듭제곱하여 정수로 만든 후 연산
const factor = 10; // 스케일 팩터
const x = 0.1 * factor; // 1
const y = 0.2 * factor; // 2
const num1 = (x + y) / factor; // 0.3
const num2 = (x * y) / factor ** 2; // 0.02
Number.EPSILON
자바스크립트의 Number.EPSILON 상수는 1과 1보다 큰 숫자 사이에서 표현할 수 있는 가장 작은 차이를 나타낸다. 즉, 두 숫자 사이의 가장 작은 차이를 나타낸다. 예를 들어 1 + Number.EPSILON은 1보다 큰 가장 작은 숫자를 가리킨다.
1 + Number.EPSILON // 1.0000000000000002
Number.EPSILON 상수의 값은 대략 2.220446049250313e-16 값을 가지는데, 이는 64비트 부동소수점의 가수부에서 표현할 수 있는 가장 작은 단위 $2^{-52}$와 동일하다. 다시 말해 부동소수점에서 이 값보다 작은 수는 무시할 수 있음을 의미한다.
Number.EPSILON // 2.220446049250313e-16 -> 0.0000000000000002220446049250313
Number.EPSILON 상수는 두 숫자가 같은지 확인할 때 유용하다. 위에서 살펴봤듯 0.1 + 0.2는 0.3이 아니라 근삿값인 0.30000000000000004가 된다. 만약 이 근삿값과 0.3의 차이가 Number.EPSILON 보다 작다면 부동 소수점에서 식별할 수 있는 값보다 더 작기 때문에 동일한 숫자로 간주할 수 있다.
const a = 0.1;
const b = 0.2;
const c = 0.3;
const equal = Math.abs(a + b - c) < Number.EPSILON; // true
// 0.30000000000000004 - 0.3 = 0.00000000000000004
// 0.00000000000000004 < 0.0000000000000002220446049250313
레퍼런스
- CS50 - 고정 소수점(fixed point)과 부동 소수점(floating point) | 생각과 고민
- 부동 소수점의 이해 (1부) | Devocean
- Why does 0.1 + 0.2 = 0.30000000000000004? | Julia Evans
글 수정사항은 노션 페이지에 가장 빠르게 반영됩니다. 링크를 참고해 주세요
'🪄 Programming' 카테고리의 다른 글
| [Algorithm] 최소 힙(Heap)으로 우선순위 큐 구현하기 (0) | 2024.05.28 |
|---|---|
| [Algorithm] 다익스트라 알고리즘 — 최단 경로 찾기 (0) | 2024.05.28 |
| [Algorithm] 유클리드 알고리즘 / 소인수분해로 최소공배수 최대공약수 계산하기 (0) | 2024.05.26 |
| [TS] 타입스크립트 구조적 타이핑 활용하기 (0) | 2024.05.25 |
| [Algorithm] 땅따먹기 알고리즘 / 동적 계획법 (2) | 2024.05.25 |
댓글
이 글 공유하기
다른 글
-
[Algorithm] 최소 힙(Heap)으로 우선순위 큐 구현하기
[Algorithm] 최소 힙(Heap)으로 우선순위 큐 구현하기
2024.05.28 -
[Algorithm] 다익스트라 알고리즘 — 최단 경로 찾기
[Algorithm] 다익스트라 알고리즘 — 최단 경로 찾기
2024.05.28 -
[Algorithm] 유클리드 알고리즘 / 소인수분해로 최소공배수 최대공약수 계산하기
[Algorithm] 유클리드 알고리즘 / 소인수분해로 최소공배수 최대공약수 계산하기
2024.05.26 -
[TS] 타입스크립트 구조적 타이핑 활용하기
[TS] 타입스크립트 구조적 타이핑 활용하기
2024.05.25